この記事から分かること
- UniswapV3の流動性提供の仕組み
- UniswapV3の変動損失の仕組み
- UniswapV3の変動損失金額
※本記事へのコメント・質問等は私のX(旧ツイッター)にDMで送っていただいても大丈夫です。丁寧に回答させていただきます。
ユニスワップV2は、2021年5月5日にユニスワップV3にアップデートされました
多くの分散型取引所で同じ仕組みが導入されており、例えば2023年4月4日にパンケーキスワップがユニスワップV3をベースとしたパンケーキスワップV3をローンチしました。
V3の「流動性マイニング」では事前に価格帯を設定して流動性を提供する点が特徴で、このように提供される流動性は特に「集中流動性」と呼ばれ、現在の分散型取引所の仕組みの主流になっています。
※従来の分散型取引所では全価格範囲(0から∞)で流動性を提供していた。

結論、V3のインパーマネントロスの発生額は従来の「V2のインパーマネントロス」と比べて大きいです。
流動性を提供する価格帯が狭ければ狭いほど大きくなり、V2と比べた時のインパーマネントロスの発生倍率は下のように異なります。(BTC&USDTの流動性提供の例)

数倍~数十倍のインパーマネントロスは簡単に発生するため、注意が必要です。
 さとう
さとう本記事を最後まで読むと、V3のインパーマネントロス発生の仕組みと計算方法が分かります。
※ユニスワップV3の仕組みが他の分散型取引所にも採用されているため、本記事の内容は他の分散型取引所のV3の仕組みにも対応しています。
本記事の関連記事
本記事は、以下のリサーチ記事とUniswapV3のホワイトペーパー&開発仕様書を参考に作成しています。
UniswapV3の流動性提供の仕組みの概要


UniswapV3のインパーマネントロスの解説の前に、まずUniswapV3とV2の流動性提供の変更点をご紹介します。
UniswapV3には、従来のUniswapV2とは異なる5つの特徴があります。
- Uniswap V3では価格帯を決めて提供
- 価格帯に該当してると手数料が貰える
- スワップ手数料は流動性提供者が決定
- 価格帯毎に異なる流動性のカーブ
- 流動性を1:1の等価で提供する必要はない



詳しい内容は下の「UniswapV3とV2の違い解説記事」でご紹介しているので、こちらをご覧下さい。


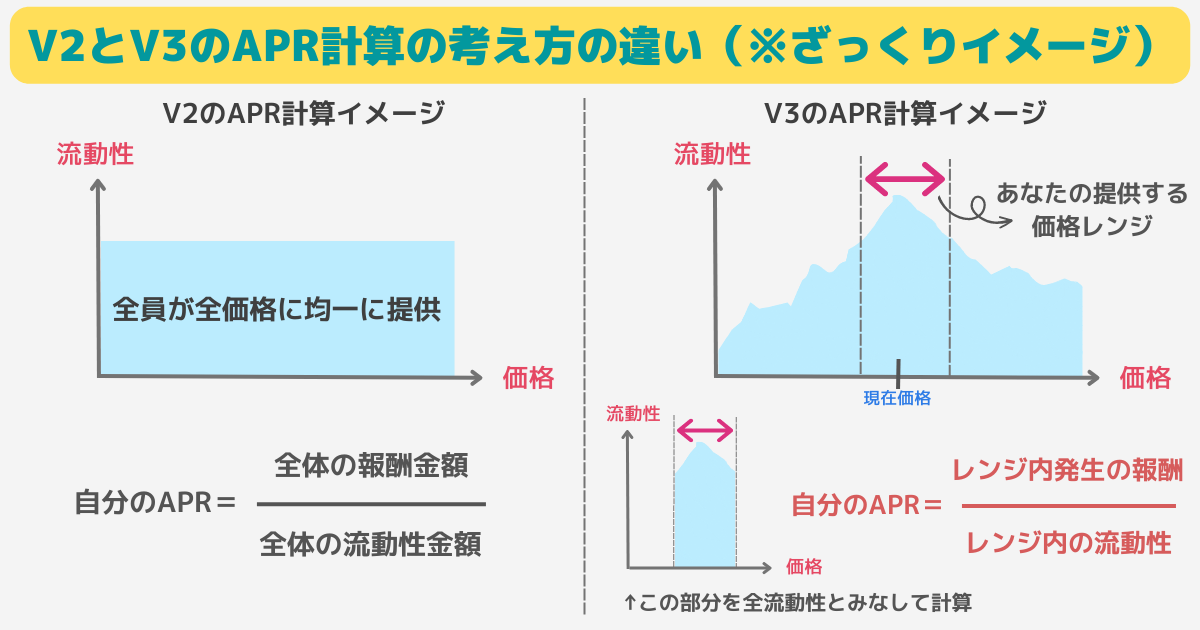

集中流動性の流動性提供の仕組みについても、上記の記事で詳しく解説しています。
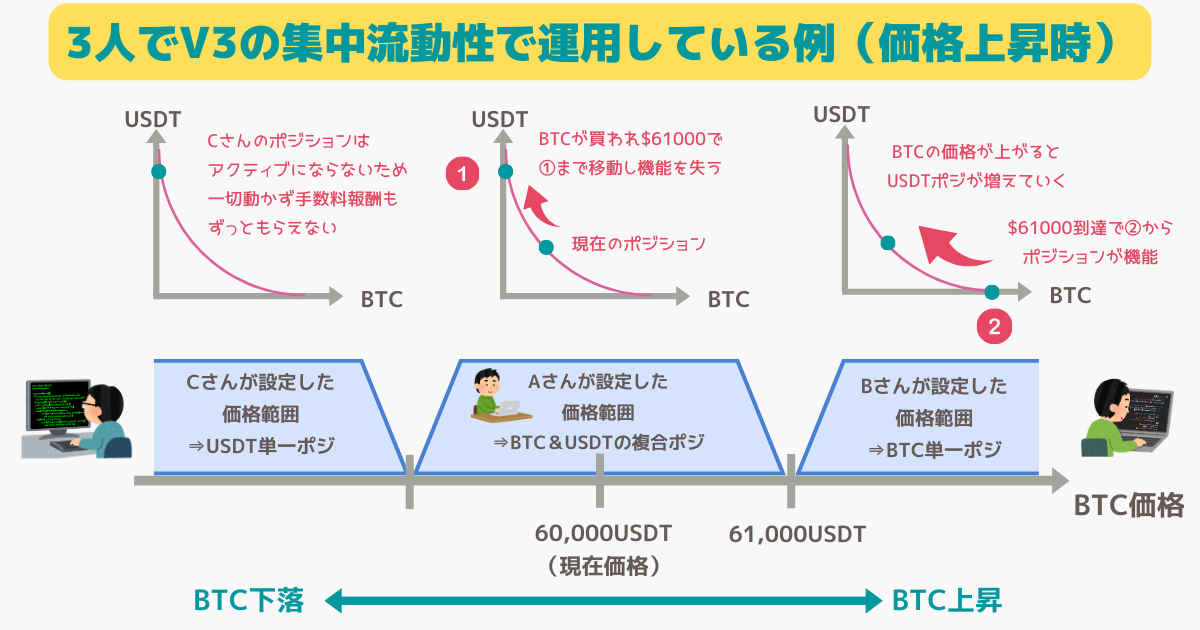

UniswapV3のインパーマネントロスとは


UniswapV3のインパーマネントロスの仕組みをご紹介します。



以下の流れで話を進めます。
- UniswapV2と比べてV3の変動損失は大きい
- UniswapV2のAMMの簡単なおさらい
- UniswapV3の流動性提供の式を解説
- V3のインパーマネントロスを計算してみる
UniswapV2と比べて変動損失は大きい
結論、UniswapV3のインパーマネントロスはUniswapV2と比べて大きいです。
提供する流動性の設定価格帯を狭くすればするほど、インパーマネントロスは増えます。
V3のインパーマネントロスの発生倍率は、V2と比べると下のようにで大きくなります。


V3で価格範囲を決めて流動性を提供する場合は、価格が変化しやすいペアであるほど提供する流動性の金額を小さくする必要があります。
狙った価格帯で流動性が利用されれば、提供する流動性の金額が小さくてもスワップ手数料を従来のV2と比べて多くもらえる仕組みです。



UniswapV3は「資本効率性(Capital Efficiency)」を重視しているため、このように流動性を無駄に提供しづらい環境にしています。
ここから、UniswapV3のインパーマネントロスが従来と比べて大きい理由を解説します。
UniswapV2の簡単なおさらい
UniswapV2の流動性の仕様を簡単に解説します
UniswapV2では、次の式に従って流動性の枚数や仮想通貨の価格が変化していました。
\(xy=k\)
流動性が新規で提供されたり、削除されたりする時にkが再計算され、流動性提供プールのペアxとyの枚数は常にxy=kのグラフに従って変化していきます。(Constant Product AMM)
UniswapV3の流動性提供の式
UniswapV3の流動性では、次の式をベースに考えます。
\(xy=L^2\)



このままではV2と同じになってしまうので、V3の特徴を表現するために、このグラフを変形してます。
UniswapV3の流動性は価格レンジを設定し、上限または下限に達すると片方の流動性しか提供する必要がないことが特徴の1つでした。(資本効率性を重視)
この特徴を式に反映させます。
イメージしやすくするために、今回提供する流動性の枚数はBTC(x)&USDT(y)で考えます。ビットコインの流動性提供枚数がx、ステーブルコインUSDTの流動性提供枚数がyです。
ビットコインの価格をPとすると、Pは次のように表せます。
\(P=\frac{y}{x}\)
このとき、xとyはそれぞれLとPを使って次のように表せます。
①:\(xy=L^2\)
②:\(y=Px\)
上記の2式より、\(x=\frac{L}{\sqrt{P}}\)
①:\(xy=L^2\)
②:\(y=Px\)
上記の2式より、\(y=L\sqrt{P}\)
UniswapV3の流動性は価格範囲を設定し、上限または下限に達すると片方の流動性しか提供する必要がないことが特徴でしたが、これは次のようなグラフです。
- \(xy=L^2\)のグラフを-x方向に\(\frac{L}{\sqrt{Pb}}\)だけ平行移動する
- \(xy=L^2\)のグラフを-y方向に\(L\sqrt{Pa}\)だけ平行移動する
Pbは上限設定した価格、Paは下限設定した価格です。
平行移動させたグラフとその式が次の通りです。



平行移動のとき、符号の向きは逆になります。
\((x+\frac{L}{\sqrt{Pb}})(y+L\sqrt{Pa})=L^2\)
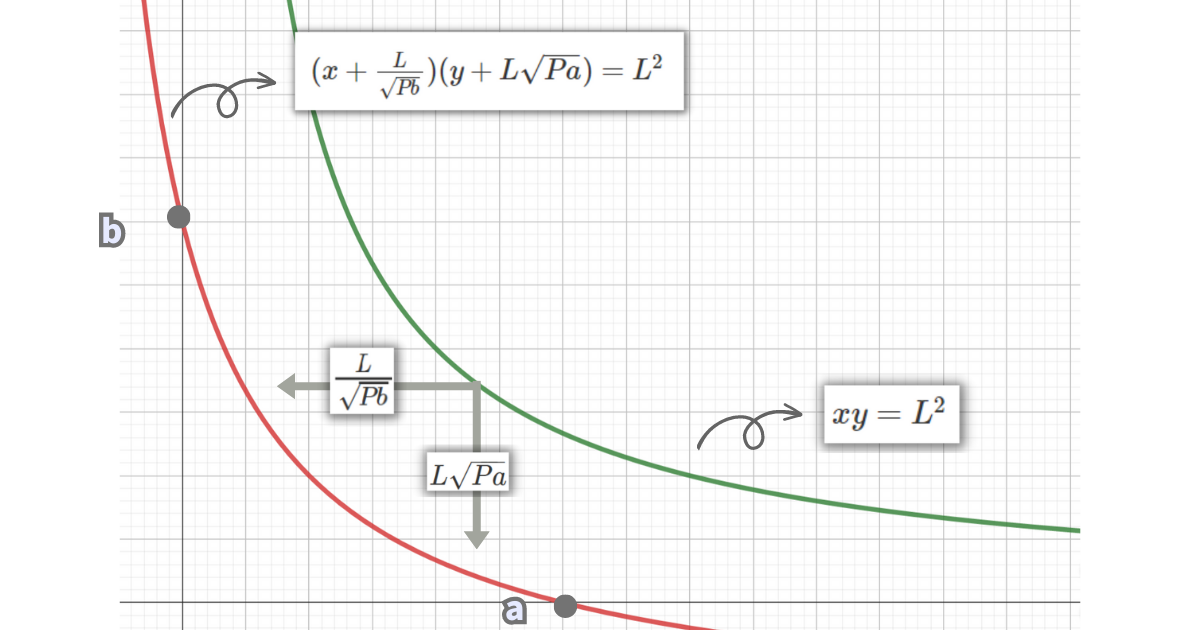

ビットコインの価格が上限になったときにx(BTCの枚数)がゼロになるグラフというのは、\(xy=L^2\)を\(\frac{L}{\sqrt{Pb}}\)分だけ平行移動したグラフのことです。
そして、ビットコインの価格が下限になったときにy(USDTの枚数)がゼロになるグラフというのは、さらに\(xy=L^2\)を\(L\sqrt{Pa}\)分だけ平行移動したグラフのことです。



だからこのようなグラフになる訳ですね。
ここで別にもう一つ、次の式が成り立つことの証明をしておきます。(後で使います)
\(\Delta y=L・\Delta\sqrt{P}\)
\(\Delta x=L・\Delta\frac{1}{\sqrt{P}}\)
先程平行移動して作ったグラフは、流動性として提供するxとyの枚数を決めるための専用のグラフです。
UniswapV3では、このグラフはあなたにとってのリアルカーブ(Real Curve)と呼ばれます。
平行移動する前のグラフは、対照的にバーチャルカーブ(Virtual Curve)呼ばれます。
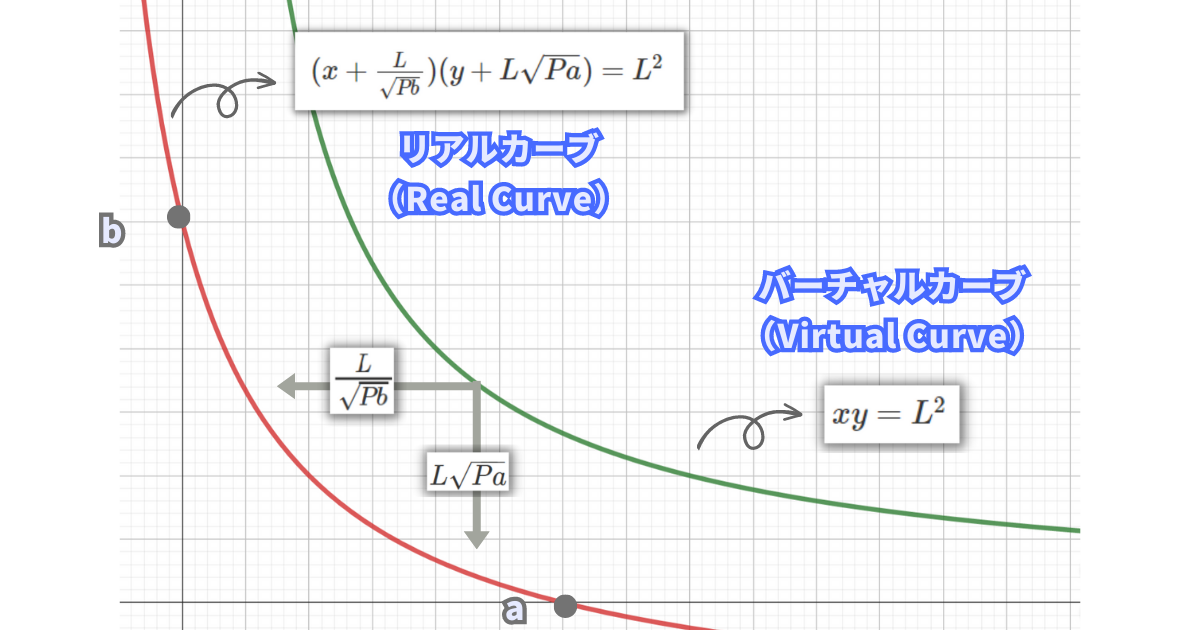

今回証明する式では、Real CurveとVirtual Curveで定義される値が混在します。
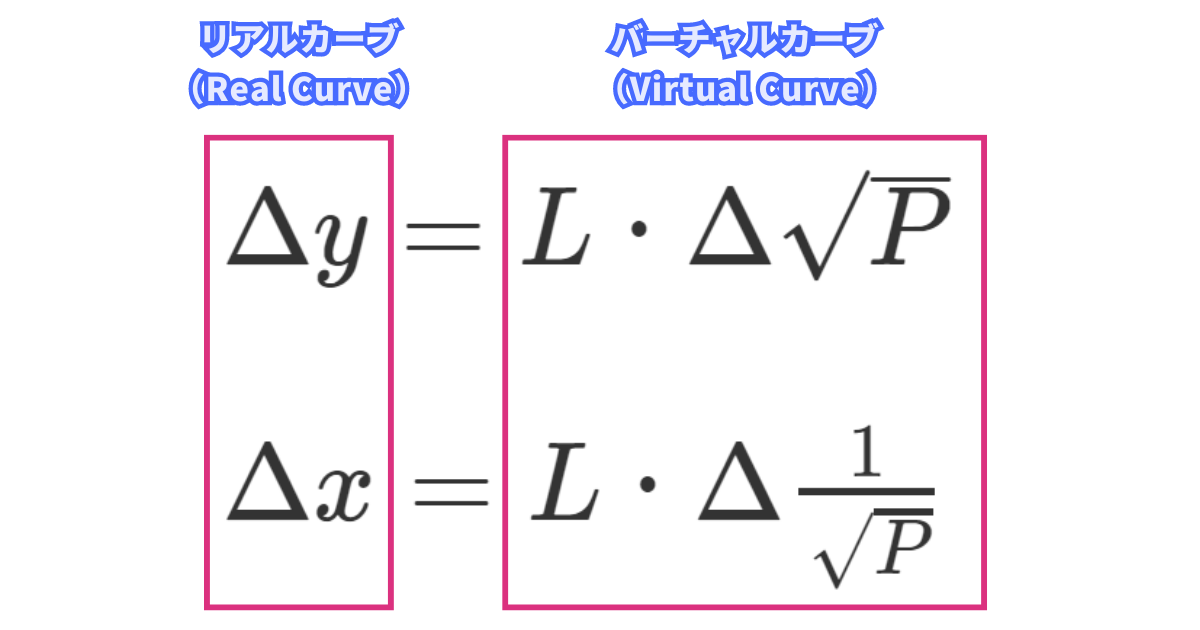
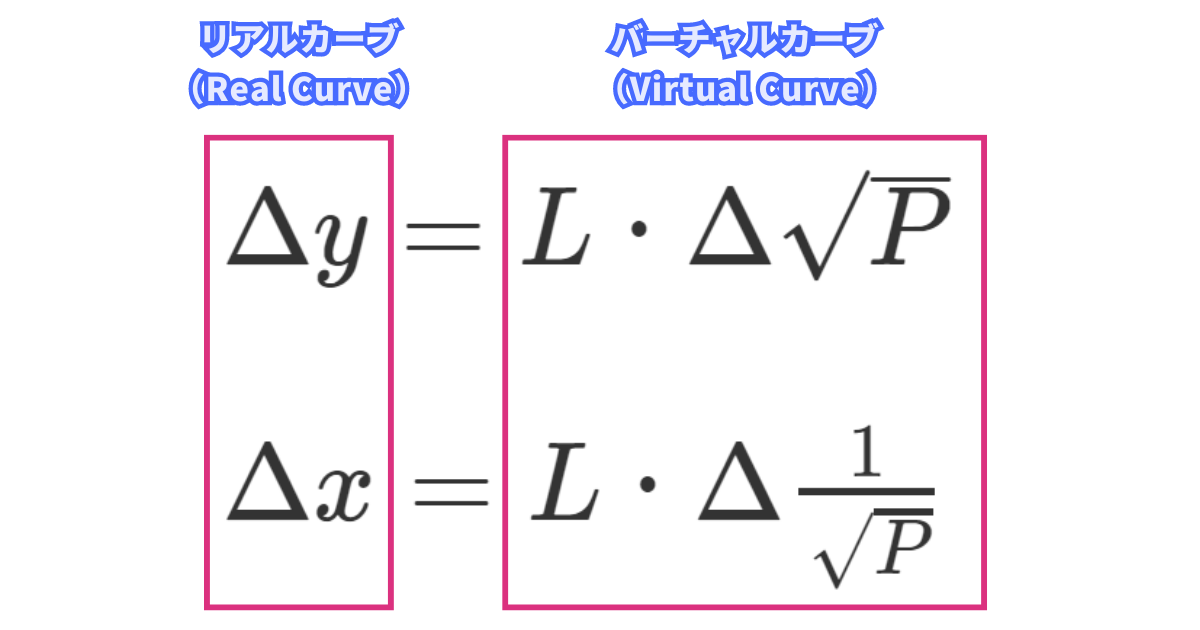
Δyはあなたが提供するUSDTの枚数なので、Real Curveで決定されます。
Lは平行移動する前の\(xy=L^2\)で定義したので、Virtual Curve上で決定されて固定です。
V3では流動性を等価で提供する必要はないので、ΔPはReal Curve上で定義される値ではなく、Virtual Curve上で得られる値であることが分かります。
言い換えると、あなたが提供する流動性の枚数をVirtual Curve上に戻すと現在価格を表します。
つまり、提供する流動性の変化Δyは、Virtual Curve上のPの変化ΔPで求まります。(Lは固定)
証明の過程も載せておきます。
\(\Delta Y=L・\Delta\sqrt{P}\)
\(\sqrt{xy}=\frac{y_{1}-y_{0}}{\sqrt{P_{1}}-\sqrt{P_{0}}}\)
\(\sqrt{xy}(\sqrt{P_{1}}-\sqrt{P_{0}})=y_{1}-y_{0}\)
\(\sqrt{xy}(\sqrt{\frac{y_{1}}{x_{1}}}-\sqrt{\frac{y_{0}}{x_{0}}})=y_{1}-y_{0}\)
Virtual Curve上では、\(\sqrt{x_{1}y_{1}}=\sqrt{x_{0}y_{0}}=\sqrt{xy}=L\)のため、
\(\sqrt{\frac{x_{1}y_{1}y_{1}}{x_{1}}}-\sqrt{\frac{x_{0}y_{0}y_{0}}{x_{0}}}=y_{1}-y_{0}\)
\(\sqrt{y_{1}^2}-\sqrt{y_{0}^2}=y_{1}-y_{0}\)
\(y_{1}-y_{0}=y_{1}-y_{0}\)
Δxについても同様です。



証明した式は後で使うので、少しの間忘れていても大丈夫です。
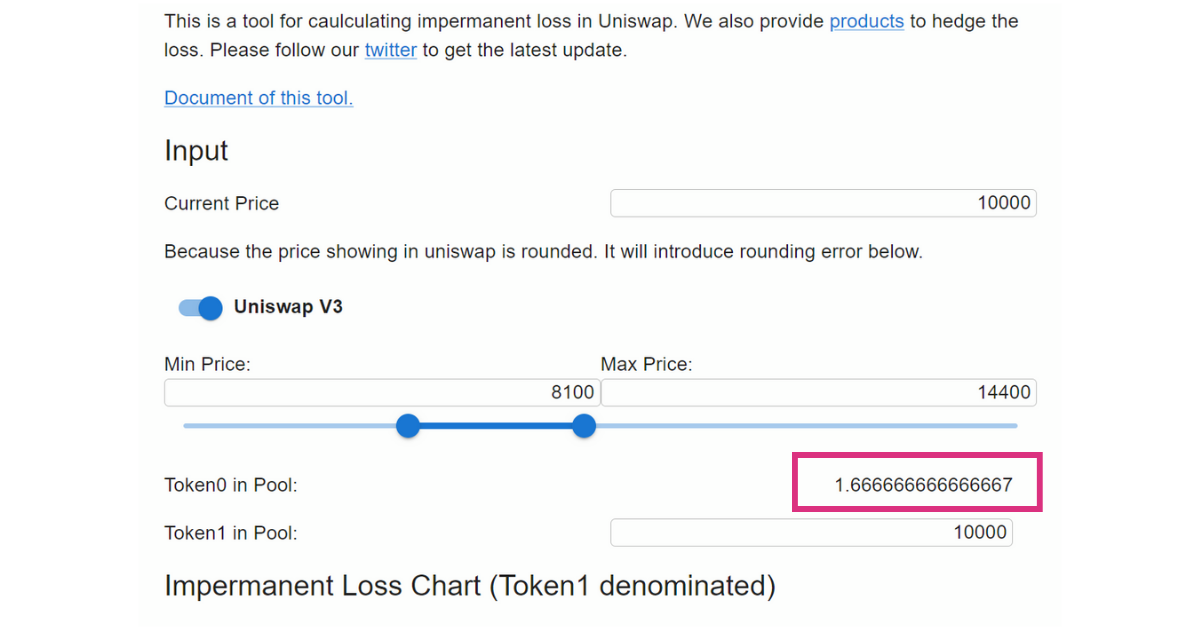
ここまでの式を使い、次の条件で10,000USDTを流動性提供した時のBTCの提供枚数を求めてみます。
- 提供しようとしている流動性:BTC&USDT
- 現在のBTCの価格:10,000USDT/BTC
- 流動性の上限価格:14,400USDT/BTC
- 流動性の下限価格:8,100USDT/BTC
- 提供するUSDTの枚数:10,000USDT
- 提供するBTCの枚数:?(ここを求める)
Real Curveの式のyに10,000を入れれば良さそうですが、Lが分からないので計算できません。
\((x+\frac{L}{\sqrt{Pb}})(y+L\sqrt{Pa})=L^2\)
ここで忘れていた次の証明済みの式を思い出してみます。
\(\Delta y=L・\Delta\sqrt{P}\)
\(\Delta x=L・\Delta\frac{1}{\sqrt{P}}\)



流動性の変化を表すReal Curve上のxとyの変化は、Virual Curve上のPの変化とLで表せることが証明できたんだよね。
例えばyの式の方に着目すると、今回追加する流動性ΔyはLとΔPで示せます。



このΔyの式に当てはまるΔPは、簡単に求められます。
今回追加する流動性Δy分は仮に全て買われる(ETHが売られる)時、現在の流動性を表す地点がcだとすると、aまで移動してきます。
これはVirual Curveのグラフで考えると、現在価格(Pc)から下限価格(Pa)まで移動していることにもなります。
※資本効率性の観点から、価格Paまで行ったときにyは必要なくなるというUniswapV3の流動性の定義をしっかり表している。
つまり、Δyに対応するΔPは、\(Pc-Pa\)であるという訳です。
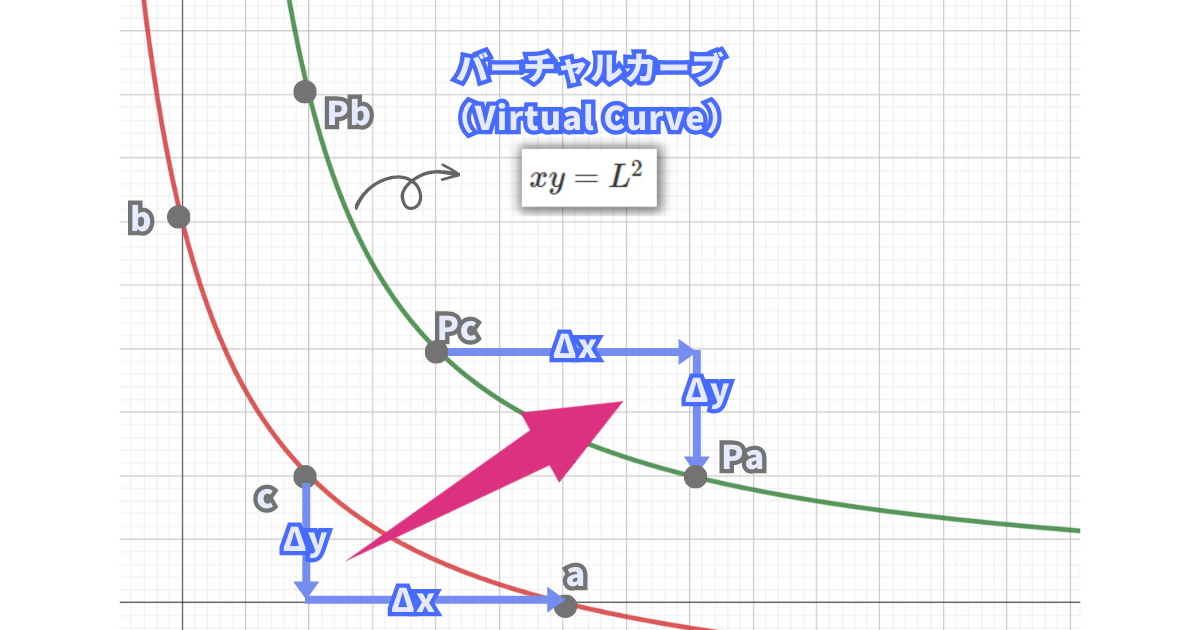

同じように考えると、Δxに対応するΔPは、\(\frac{1}{\sqrt{Pc}}-\frac{1}{\sqrt{Pb}}\)となります。
証明した式のΔPにそれぞれを当てはめると、次のようになります。
\(\Delta x=L(\frac{1}{\sqrt{Pc}}-\frac{1}{\sqrt{Pb}})\)
\(\Delta y=L(\sqrt{Pc}-\sqrt{Pa})\)
例題の値を当てはめると、次のようになります。
\(\Delta x=L(\frac{1}{\sqrt{10000}}-\frac{1}{\sqrt{14400}})\)
\(10000=L(\sqrt{10000}-\sqrt{8100})\)
最初にLが1000であることが分かり、ビットコインの提供枚数(Δx)=1.6666…であることが分かります。
今回の例では設定した価格帯の中で現在価格は下限価格に寄っているため、ビットコインの価格が上がったときに利用されやすい流動性の提供方法ということです。
ビットコインの価格が上がった時というのは、ビットコインの枚数が流動性から少なくなったときであり、V3の資本効率性の観点から考えると、よりビットコインを必要としている状況ということです。



従って、提供するビットコインの枚数はUniswapV2の時に計算される1BTCより多くなります。
「V3のインパーマネントロスシミュレーションツール」を使うと、同じようにBTCの提供枚数は1.666666と出力されることが分かります。




気になる方は是非突合してみて下さい。
ちなみに平行移動させたグラフ上のxとyから、Lを直接求めることはできません。
今回例に挙げたx=1.6666….とy=10,000からLは計算できないということです。
これは、Lは平行移動する前のグラフ(Virual Curve)で定義した時の値だからです。
x=1.6666….とy=10,000をそれぞれ\(\frac{L}{\sqrt{Pb}}\)、\(L\sqrt{Pa}\)分戻したXとYからLは計算され、流動性を提供したときに裏で計算されているので、本記事でLの具体的な値を意識する必要はありません。
解説③:インパーマネントロスの計算
UniswapV3の流動性提供の基本が分かった所で、早速インパーマネントロスを計算します。



先程の例題を元に、インパーマネントロスがどれくらい発生するか具体的に計算してみます。
流動性を提供した後の価格変化による自分の流動性プールの変化は、解説②で紹介した式に変化後の価格を入れるだけで簡単に計算されます。
例えば1BTCの価格が10,000USDTから12,000USDTになったときは次のように計算できます。(1.2倍)
\(\Delta x=L(\frac{1}{\sqrt{Pf}}-\frac{1}{\sqrt{Pb}})\)
\(\Delta y=L(\sqrt{Pf}-\sqrt{Pa})\)
Pf:将来価格(価格変化後)
\(\Delta x=1000(\frac{1}{\sqrt{12000}}-\frac{1}{\sqrt{14400}})\)
\(\Delta y=1000(\sqrt{12000}-\sqrt{8100})\)
x=0.79537…
y=19,544…



流動性を提供した時にLが1000であることが分かっているので、今回は簡単に計算できました。
合計金額は「0.79537×12000+19544=29,088ドル」となりました。
流動性を提供していなかった場合は「1.66666×12000+10000=30,000ドル」でした。
従ってインパーマネントロスの割合は912/30000=約3%です。
価格が1.2倍になったときに発生するインパーマネントロスはUniswapV2では約0.4%だったので、7.5倍のインパーマネントロスが発生しています。
設定した価格レンジが狭ければ狭いほどインパーマネントロスは大きくなり、広くすれば従来のV2のインパーマネントロスの発生の仕方に近づきます。



どれくらいの価格範囲にすればいいのかな?目安が欲しいね。



V3のインパーマネントロスの発生傾向を一般化してみます。
発生するインパーマネントロスの割合は次の式で計算できます。
\(変動損失=\frac{価格変化後の流動性金額-ガチホ時の金額}{ガチホ時の金額}\)
流動性を提供した時点の流動性金額の合計をV0、価格変化後の提供した流動性の金額をV1、流動性を提供していなかった場合の金額をVheldとします。
このときV0は、現在価格Pを使って次のように表せます。
解説②より、xは\(x=L(\frac{1}{\sqrt{P}}-\frac{1}{\sqrt{Pb}})\)、yは\(y=L(\sqrt{P}-\sqrt{Pa})\)なので、V0はさらに次のように表せます。
V0の式はL・P・Pa・Pbの4つで構成される式で、P以外の3つは流動性を提供する時に決まった値で固定です。
つまり、Pを将来価格に置き換えるだけでV0の式はV1の式になります。
将来価格を現在価格Pをk倍したPkとしたとき、V1は次の通りです。
Vheldは、Pkを使って次のように表せます。
UniswapV3のインパーマネントロスの割合をILa,b(k)とすると、次のように表せます。
UniswapV2のインパーマネントロスの割合をIL(k)すると、IL(k)は\(\frac{2\sqrt{k}-1-k}{1+k}\)で表すことができるので、この値でILa,b(k)の計算結果を無理矢理括ると次のようになります。
現在価格P、レンジ下限Pa、レンジ上限Pbを入れて将来価格が何倍になったかを表すkを入れると、UniswapV3のインパーマネントロスがUniswapV2のインパーマネントロスに対して何倍か分かる式が完成しました。



これだけではまだイメージしづらいので、シチュエーションを限定して、V3のインパーマネントロスのイメージを掴みます。
本記事では価格範囲が上限と下限で等間隔の比率になっている時のインパーマネントロスを想定します。(実際のUniswapV3の流動性提供の戦略としても妥当なもの)
まず、次の2つの式を満たすようなnを決めます。



等間隔(比率)で価格レンジが広くなるとnも大きくなるんだね。
例えば次のような価格レンジを想定した場合、n=1.23…(1/n=0.81)となり、提供する流動性は等価になります。
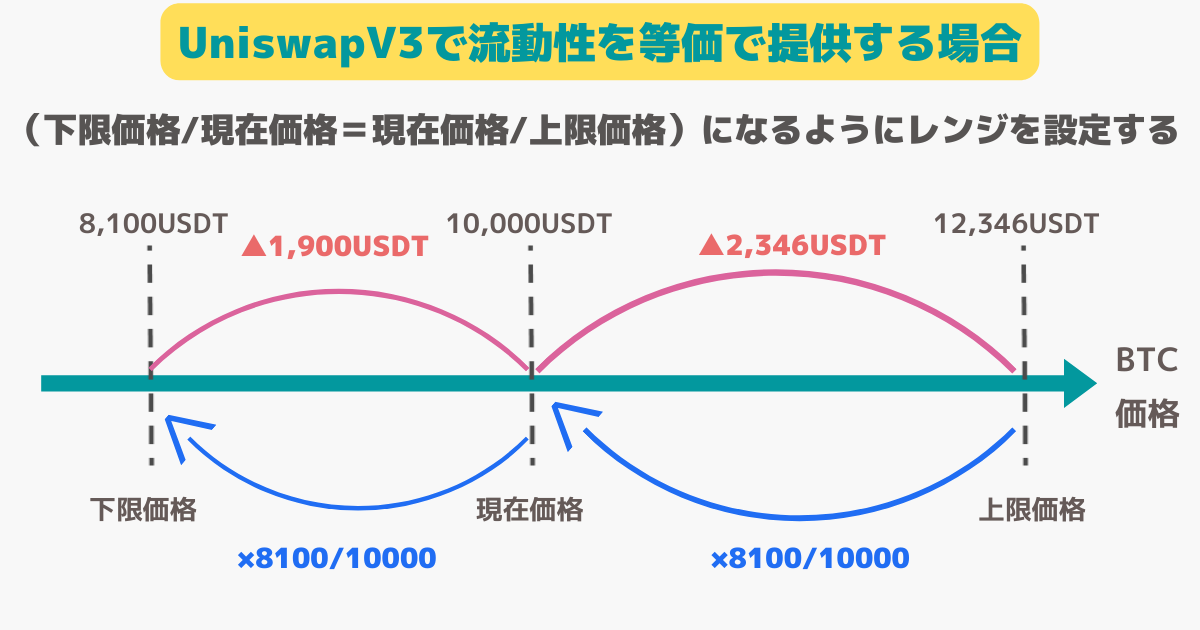

この2つの式をILa,b(k)の式に代入すると、次の式が得られます。
この式より、等間隔(比率)で価格レンジを設定したとき、UniswapV3がUniswapV2のインパーマネントロスと比べて何倍大きいかはその価格レンジの広さを表すnによって示せることが分かりました。
\(f(n)=\frac{1}{1-\frac{1}{\sqrt{n}}}\)(n>1)のグラフとnの値毎の倍率のテーブルは次のようになります。
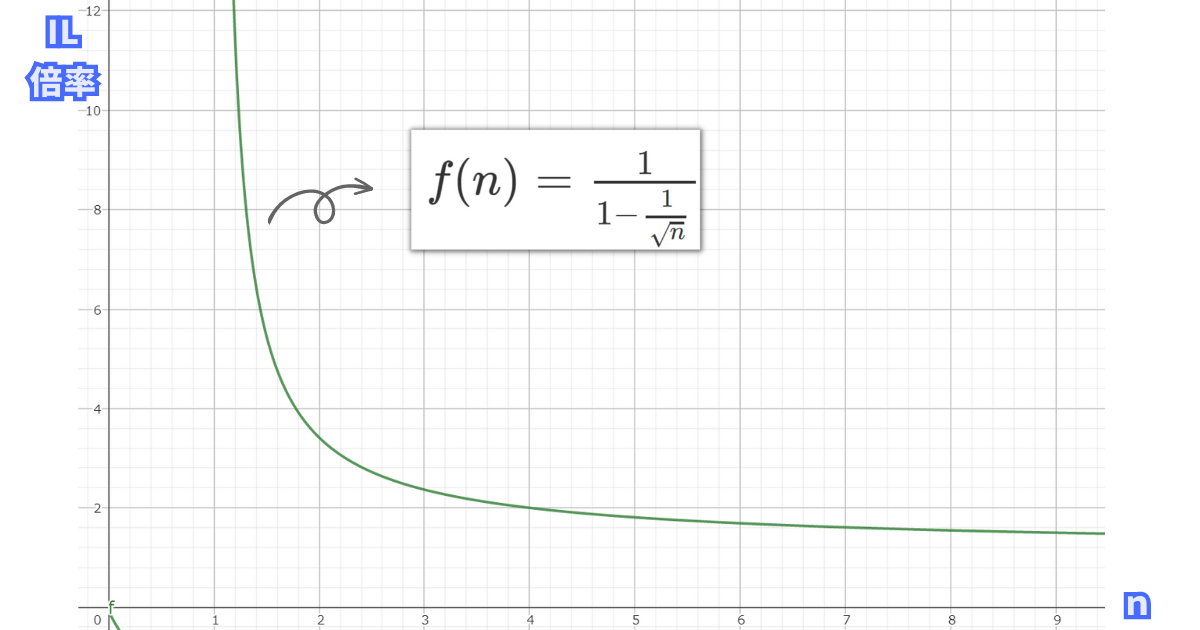

| nの値 | ILの発生倍率(V2比) |
|---|---|
| n=1.2 | 11.5倍 |
| n=1.5 | 5.4倍 |
| n=2.0 | 3.4倍 |
| n=4.0 | 2.0倍 |
UniswapV2のインパーマネントロスの早見表を下に載せておきます。



V2のインパーマネントロス早見表と、V3の発生倍率を掛け合わせることで大体の変動損失がイメージできます。
- 1.25倍の価格変動 = 0.6%の損失
- 1.50倍の価格変動 = 2.0%の損失
- 1.75倍の価格変動 = 3.8%の損失
- 2倍の価格変動 = 5.7%の損失
- 3倍の価格変動 = 13.4%の損失
- 4倍の価格変動 = 20.0%の損失
- 5倍の価格変動 = 25.5%の損失
nが2以上になるような価格範囲を取れば、インパーマネントロスはUniswapV2の3倍程度で収まります。
あとはAPR(年間利率)を考慮して、リスクに見合う流動性提供になるか検討しましょう。
目安となる価格レンジの幅とインパーマネントロスがUniswapV2の何倍になるかの図も載せておきます。


まとめ:リスクを理解して利用しよう


UniswapV3のインパーマネントロスシミュレーションは、こちらのサイトが便利です。


本記事の内容を全て理解していないくても、条件毎のインパーマネントロスは算出できるはずです。
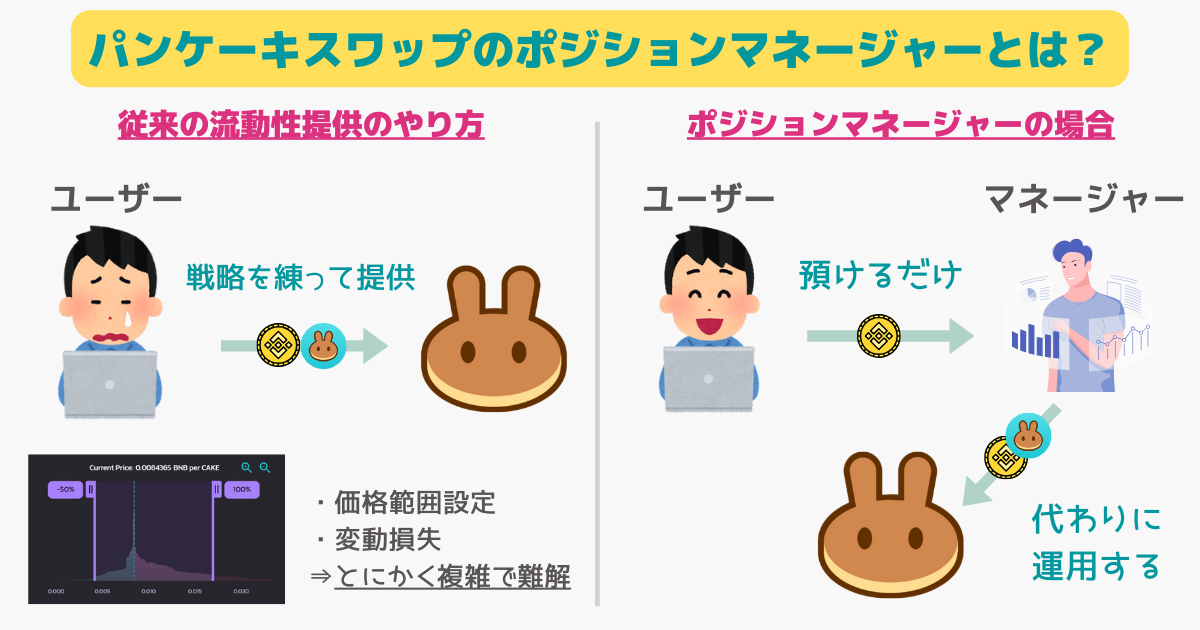
V3形式のインパーマネントロスの運用はリスクが大きいので、この問題を解決したパンケーキスワップの「ポジションマネージャー」を当サイトではおすすめしています。



V3の運用を運用の専門団体が代わりに行ってくれるので、リスクを抑えて効率よく流動性マイニングを行えます。



| パンケーキスワップの関連記事はこちら | |
|---|---|
| 使い方・始め方のまとめ | スワップのやり方 |
| ステーキングのやり方 | 草コインの買い方 |
| ポジションマネージャー | メタマスクを接続できない |
| シンプルステーキング | 報酬の収穫タイミング |
| 儲け方・手数料負けしない方法 | V3とV2の違い |
| ユニスワップの関連記事はこちら | |
|---|---|
| スワップのやり方 | ステーキングのやり方 |
| V3とV2の違い | V3のインパーマネントロス |




コメント