※本記事へのコメント・質問等は私のX(旧ツイッター)にDMで送っていただいても大丈夫です。丁寧に回答させていただきます。
StableSwap AMM(ステーブルスワップ AMM)とは、名前の通り分散型取引所のステーブルコイン同士のスワップ時の価格を決める仕組みです。
一般的に分散型取引所の仮想通貨のスワップ価格は流動性プールの中にある仮想通貨の枚数比で決まります。(xy=k)
スワップが行われると流動性の枚数比が変化し、スワップレート(仮想通貨の価格)も変わる訳です。
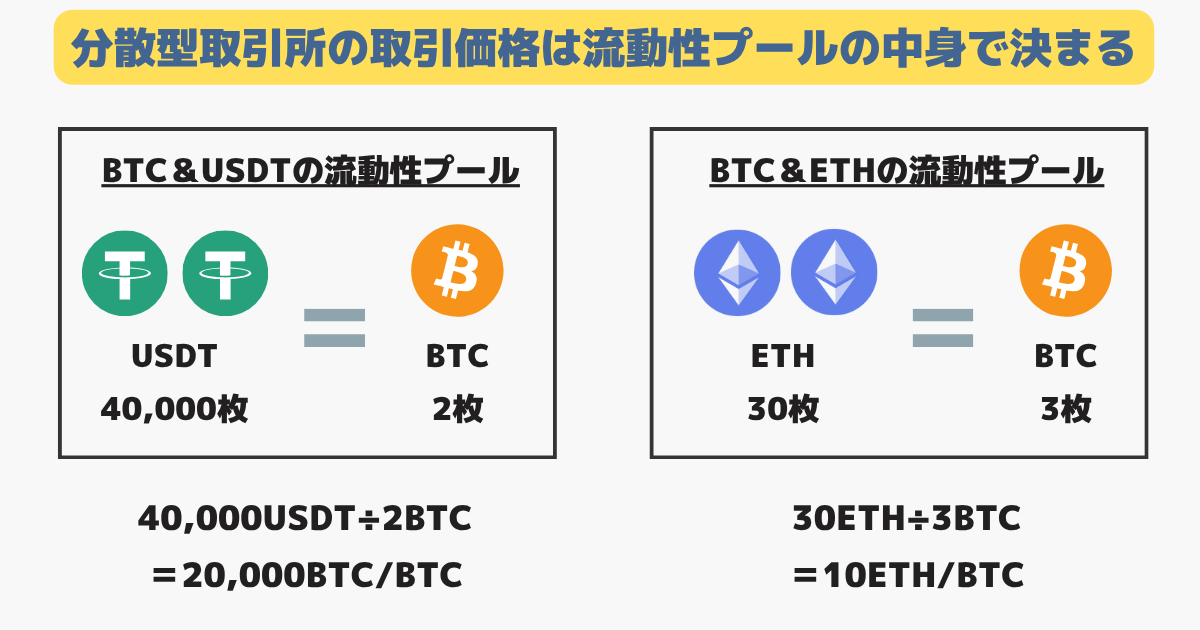
しかし、同じ価値を持つステーブルコイン同士は常に1:1でスワップされるべきなので、このルールは適しません。
 さとう
さとうそこで開発されたのが、StableSwap AMMです。
2020年1月にローンチされた分散型取引所「Curve Finance」で初めて導入され、UniswapやPancakeswap等の主要DEXでのステーブルコイン同士のスワップでも幅広く利用されています。
本記事はCurve Financeのホワイトペーパーを参考に作成しています。


StableSwapの元になる2つのAMM


StableSwap AMMは、次の2つのAMMを組み合わせた仕組みになっています。
- Constant Product AMM
- Constant Sum AMM
Constant Product AMMとは
Constant Product AMM(定積AMM)は、xy=kの式に従って流動性を管理する仕組みで、次の特徴があります。
- 仮想通貨の価格が需要に従い動く
- プールが枯渇しない
- ステーブルコインの価格も動く
Constant Product AMMは次の式で表されます。
\(xy=k\)


※xとyは流動性プール内の仮想通貨ペアそれぞれの枚数です。kは流動性プール毎に決まった値で変わらない定数です。
流動性プールにUSDCが4000枚、ETHが2枚ある例を考えてみます。
分散型取引所内の仮想通貨の価格は単純な割り算できまるので、このときETHの価格は2000USDC/ETHになります。



AMMの式は次のようになります。
\(xy=8000\)
ここでUSDCを1000枚をETHにスワップしてみましょう。USDCのプールが1000枚増えて5000枚になり、x(ETH)の枚数はAMMの式で決定されます。
\(5000x=8000\)
\(x=1.6\)
当初のETHは流動性プールに2枚あったので、差額の0.4枚が今回の1000USDCを1000枚スワップした時の受け取り分となる仕組みです。
価格にすると2500USDC/ETHとなり、スワップ前の2000USDC/ETHと比べると高くなっていることが分かります。
これは「プライスインパクト」と呼ばれ、定積AMMで流動性規模に対して大きいスワップを行うと、あなた自身のスワップレートが悪化します。
これにより、プールは絶対に枯渇しないようになっています。
もっと大きい例を考えてみましょう。このプールに対して16,000USDCでETHをスワップしてみます。
\(20000x=8000\)
\(x=0.4\)
差額の1.6ETHしか受け取れず、価格にすると10,000USDC/ETHです。
xy=8000は以下のようなグラフになり、ここまで例に挙げた分数型取引所のプール状況をプロットしました。


Constant Sum AMMとは
Constant Sum AMM(定和AMM)は、x+y=kの式に従って流動性を管理する仕組みです。
Constant Sum AMMの特徴は次の通りです。
- ステーブルコイン同士を常に1:1でスワップできる
- 需要が片方に偏るとプールが枯渇する
Constant Sum AMMは次の式で表されます。
\(x+y=k\)
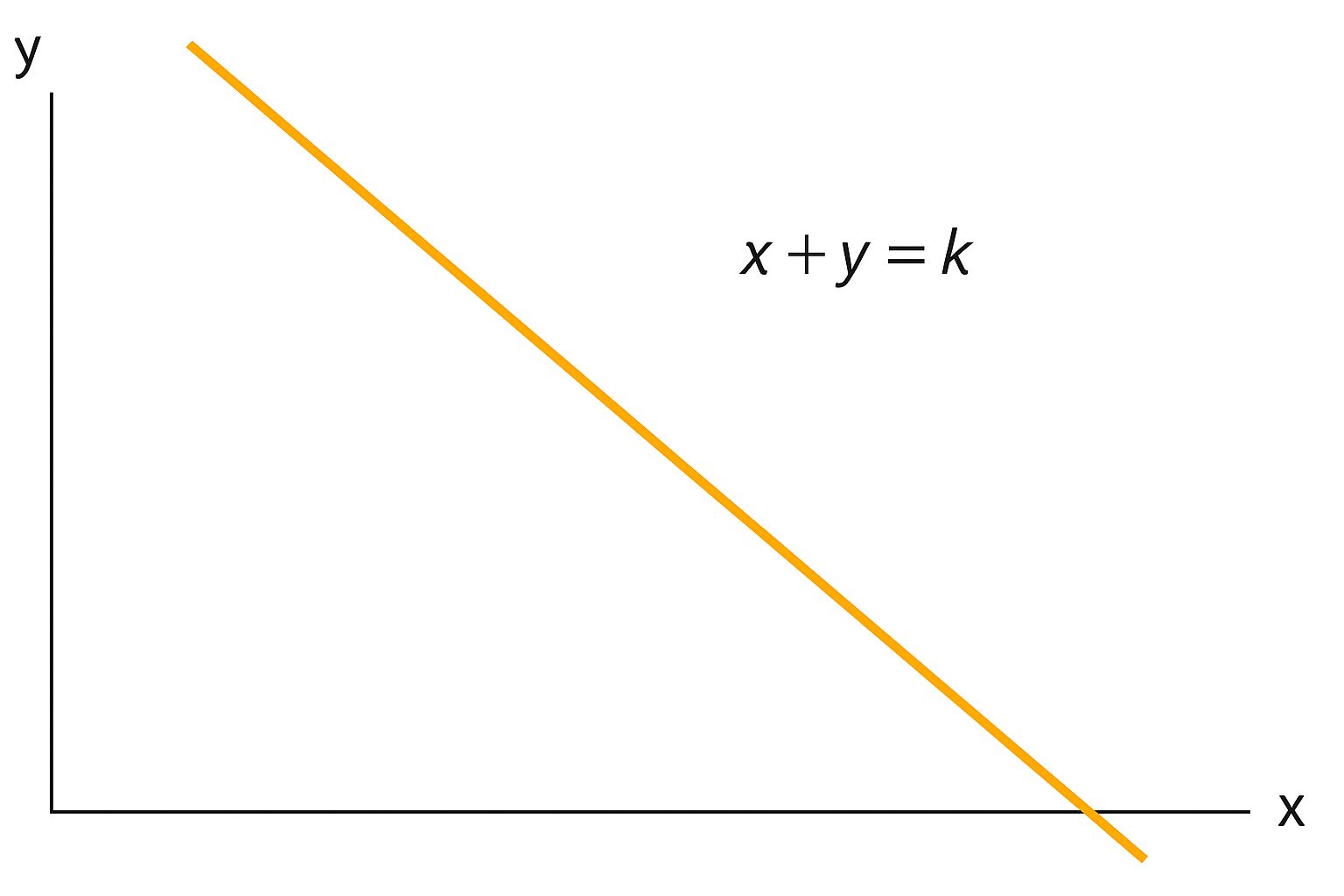

Constant Sum AMMはx+y=定数で流動性が変化するため、ステーブルコイン1枚のスワップでステーブルコイン1枚がそのまま出力されます。
しかし、片方のステーブルコインに需要が集中すれば、xかyのどちらかが空になるまで流動性が消費されてしまう可能性があるという問題があります。
Constant Product AMMはxy=定数で流動性が変化するため、片方の流動性が一方的に消費されると価格が高くなり、流動性が空になることはありません。
しかし、この仕組みステーブルコインのスワップをあてはめると1:1で交換できなくなってしまいます。
StableSwapの仕組み・計算式


StableSwap AMMは「Constant Sum AMM」と「Constant Product AMM」の2つを組み合わせて弱点を補った仕組みです。
StableSwap AMMでは流動性プールの中身が均衡している状態では仮想通貨の価格が変わらなくなり、均衡していない状態でのみ価格が変動するようになります。
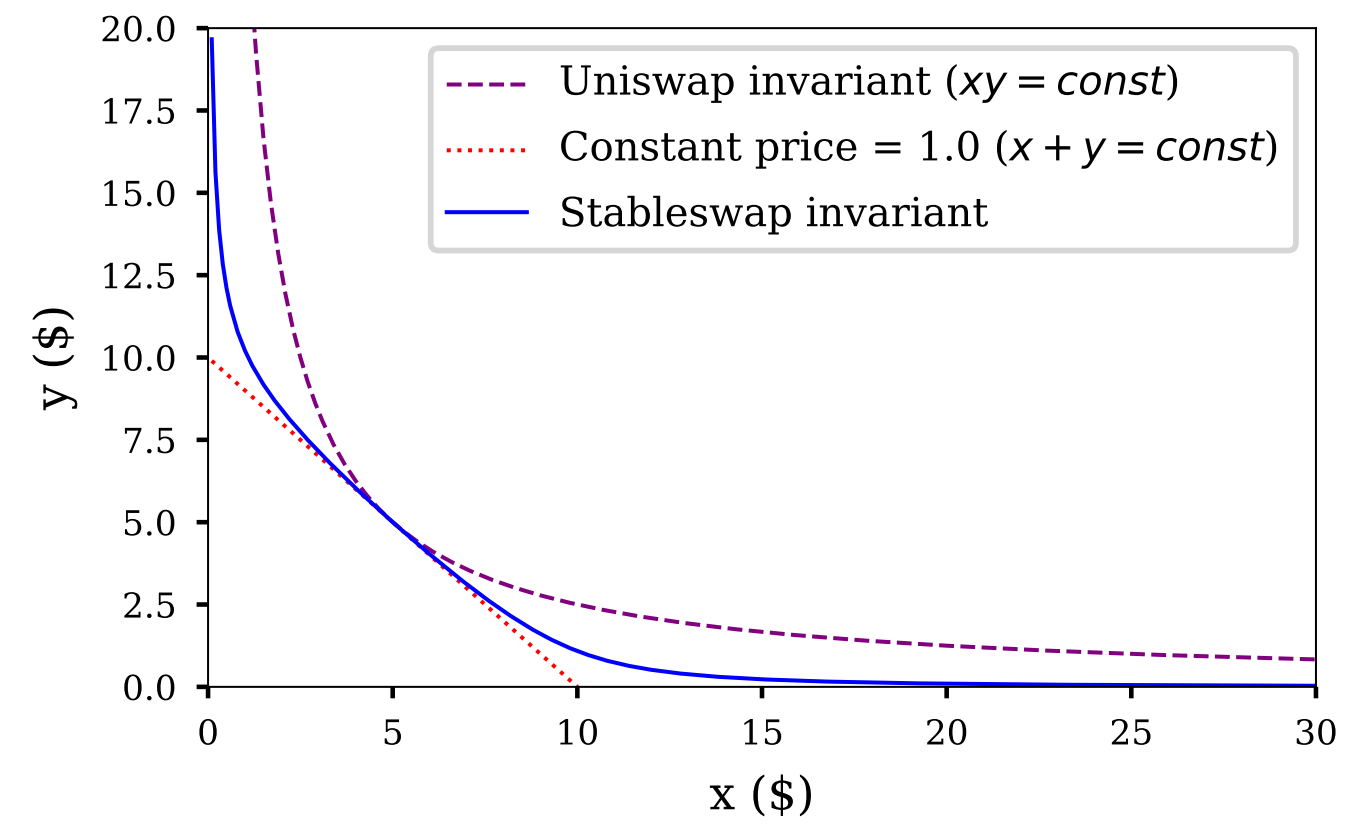

- 赤色の点線:Constant Sum AMM
- 灰色の点線:Constant Product AMM
- 青色の実線:StableSwap AMM
StaleSwap AMMの仕組みは次の式で表されます。(2種類のステーブルコインが入った流動性プールの時)
\(γD(x+y)+xy=γD^2+(D/2)^2\)
xとyは流動性プール内の2種類のステーブルコインの枚数を表しており、xとy片方の枚数変化からもう片方の枚数変化が分かるようになっています。



上記の式は次のように導出できます。
Constant Sum AMMとConstant Product AMMをそれぞれ次の式で表します。
\(x+y=D\)
\(xy=(D/2)^2\)
Dは流動性プール内の仮想通貨xとyの価格が同じになっているときのxとyの枚数の合計で、最初に流動性プールを作った時に決められます。
次に、xyをDを使って表します。
Dをプール内の仮想通貨種類の数である2で割り、2乗するとxyになります。
この2つの式をそのまま足します。
\(x+y+xy=D+(D/2)^2\)
左辺と右辺に2つのAMMの要素が組み合わさりました。ここでConstant Sum AMMの要素にγ(ガンマ)を掛けます。
\(γ(x+y)+xy=γD+(D/2)^2\)
あとはこのγの値がプールの中身が均衡しているときは大きくなるように、プールの中身が均衡していないときは小さくなるように設定すれば、StableSwap AMMの仕組みを式で表せます。
※StableSwap AMM:プールの中身が均衡している状態では価格が変わりづらくなり、均衡していない状態では価格が変わりやすくなるということ
γは次の式で表されます。
\(γ=A\frac{xy}{(D/2)^2}\)
Aという文字が新しく出てきましたが、こちらは後で解説しています。
Aの右の分数の部分は完全にプールの中身が均衡していると1になり、均衡から外れるとどんどん小さくなります。



以下の表で確認してみましょう。
| x | y | xy | D | \(\frac{xy}{(D/2)^2}\) | 均衡 |
|---|---|---|---|---|---|
| 100 | 100 | 10000 | 200 | 1 | ◯ |
| 99 | 101 | 9999 | 200 | 0.999 | ◯ |
| 90 | 110 | 9900 | 200 | 0.990 | ◯ |
| 30 | 170 | 5100 | 200 | 0.510 | × |
| 1 | 199 | 199 | 200 | 0.019 | × |
このようにxとyの枚数に差が出てきて均衡しなくなると、分数の値はどんどん小さくなります。
これでほとんどγ(ガンマ)の役割を表せましたが、最後にAの値を考えます。
Aの値は分散型取引所のコミュニティ(DAO)の中の投票で決まります。
例えば、あるステーブルコイン同士の流動性プールで、裏付け資産(ペグ)が外れることがない安全なコインである場合は、Aの値は大きくすれば良いことになります。
例えば、A=10のときの先程の表でγ(ガンマ)を見てみましょう。
| x | y | xy | D | \(\frac{xy}{(D/2)^2}\) | γ |
|---|---|---|---|---|---|
| 100 | 100 | 10000 | 200 | 1 | 10 |
| 99 | 101 | 9999 | 200 | 0.999 | 9.99 |
| 90 | 110 | 9900 | 200 | 0.990 | 9.90 |
| 30 | 170 | 5100 | 200 | 0.510 | 5.10 |
| 1 | 199 | 199 | 200 | 0.019 | 0.19 |
均衡しているときγは10になるので、Constant Sum AMMの影響が大きくなります。
一番下の例の場合、均衡していないためγの値は0.19になっており、Constant Sum Productの影響が大きくなります。
このようにγが均衡状態を表すことで、下の式は「プールの中身が均衡している状態では価格が変わりづらくなり、均衡していない状態では価格が変わりやすくなる」を表す訳です。
\(γ(x+y)+xy=γD+(D/2)^2\)
最後にこの式のConstant Sum AMMの要素にだけDを掛けます。
\(γD(x+y)+xy=γD^2+(D/2)^2\)
Dを掛ける理由は少し複雑です。
ステーブルコインをスワップする際のStableSwap AMMですが、このルールはプールの中身がステーブルコイン2種類ではなく、3種類・4種類とどんなプール内の種類数でも対応できる式になっています。
※StableSwap AMMの文献を出しているCurveの分散型取引所には3種類・4種類のステーブルコインが入った流動性プールが実際にあるからです。
γ(ガンマ)の値は次のように計算されました。
\(γ=A\frac{xy}{(D/2)^2}\)
流動性プール内のステーブルコインの種類の数が3個の場合、この式は次のようになります。
\(γ=A\frac{xyz}{(D/3)^3}\)
流動性プール内のステーブルコインの種類の数がn個の場合、この式は次のようになります。
\(γ=A\frac{xy・・}{(D/n)^n}\)
ここで問題になるのが、γの分母にDのn乗が入ってしまうことです。
γの値はConstant Sum AMMの影響が強い式にするか、Constant Product AMMの影響が強い式にするかに変えるためのパラメーターのような役割でした。
そこでγにはDのn-1乗を掛けるようにします。こうすることで、γの分母は必ずDになります。nが入っていないので、γは流動性プール内の仮想通貨の個数がいくつでも対応できます。
だから先程のステーブルコイン2種類の例では、Dの2-1乗としてDを掛けたという訳です。
StableSwap AMMのグラフを実際に作ってみた


ステーブルコインA・Bが100万枚ずつ提供されている流動性プールのStableSwap AMMをグラフにしてみました。
StableSwap AMMの式は次のようになります。


- Dは100万枚+100万枚=200万で固定しています。
- Aの値を動かすと、直線に見える部分を伸ばしたり、短くしたりできます。
マイナスの値もグラフで表現されてしまっていますが、Geogebraで定義する方法が分からずご容赦下さい。



ご覧いただきありがとうございました。
本記事に関するご質問・ご感想はコメント欄か下記のお問い合わせページ・XのDMよりお送り下さい。丁寧に回答させていただきます。
メールアドレスはこちら:contact@pandacrypto.xsrv.jp

ご覧いただきありがとうございました。
本記事に関するご質問・ご感想はコメント欄か下記のお問い合わせページ・XのDMよりお送り下さい。丁寧に回答させていただきます。
メールアドレスはこちら:contact@pandacrypto.xsrv.jp
※2020年5月1日より「仮想通貨」は「暗号資産」へ呼称変更されていますが、一部記事では「仮想通貨」の表記を継続する場合があります。当サイトの「仮想通貨」は「暗号資産」を指します。
仮想通貨に関する注意喚起

仮想通貨の価格は日々変動しており、保有する仮想通貨の価格が急激に下落する場合があります。購入時の価格を下回ったり、無価値になってしまうことで大きな損失が発生する恐れがあります。
仮想通貨の信用取引は、価格変動により保証金を上回る損失が発生する場合があります。
その他仮想通貨に関する注意喚起について詳しく知りたい方は、以下をご覧ください。
| 金融庁 | 暗号資産の利用者のみなさまへ |
| 警察庁 | 暗号資産(仮想通貨)に関するトラブルにご注意ください! |
| 消費者庁 | 投資などのお金に関するトラブルや悪質商法について |
| 国税庁 | 仮想通貨の税務上の取扱い-現状と課題- |
| 政府広報オンライン | 暗号資産の「必ずもうかる」に要注意! |
| 日本暗号資産取引業協会 | 暗号資産に関するトラブルにご注意ください! |
| 国民生活センター | 暗号資産に関する消費者トラブル |






コメント