🐼 当サイトのコンテンツ制作ポリシー
「ぱんだくりぷとの」のコンテンツ制作・編集ポリシーはこちらでご紹介しています。
※本記事へのコメント・質問等は私のX(旧ツイッター)にDMで送っていただいても大丈夫です。丁寧に回答させていただきます。
StableSwap AMM(ステーブルスワップ AMM)とは、名前の通り分散型取引所のステーブルコイン同士のスワップ時の価格を決める仕組みです。
基本的に、分散型取引所の仮想通貨のスワップ価格は流動性プールの中にある仮想通貨の枚数比で決まります。(USDCが4000枚、ETHが2枚のときは2000USDC/ETH)
しかし、同じ価値を持つステーブルコイン同士のスワップにこのルールは適しません。
 さとう
さとうそこで開発されたのが、StableSwap AMMです。
2020年1月にローンチされた分散型取引所「Curve Finance」で初めて導入され、UniswapやPancakeswap等の主要DEXでのステーブルコイン同士のスワップでも利用されています。
本記事はCurve Financeのホワイトペーパーを参考に作成しています。


前提:StableSwapの元になる2つのAMM


ステーブルコイン同士のスワップにおける価格を自動で決めるシステムAMM(Automated Market Makers)では、StableSwap AMMと呼ばれる方法が採用されています。
Curve以外にも多くの分散型取引所がステーブルコイン同士のスワップでこの仕組みを採用しています。
StableSwap AMMは、次の2つのAMMを基にAMMです。
- Constant Sum AMM(コンスタントサム AMM)
- Constant Product AMM(コンスタントプロダクト AMM)



先にこの2つの仕組みの概要をおさらいします。
①Constant Sum AMMとは
Constant Sum AMMは直訳すると「定和による価格自動決定システム」です。
Constant Sum AMMには、次のメリット・デメリットがあります。
- ステーブルコイン同士を常に1:1でスワップできる
- ステーブルコインでデペグが起きるとプールが枯渇
Constant Sum AMMは次の式で表されます。
\(x+y=k\)
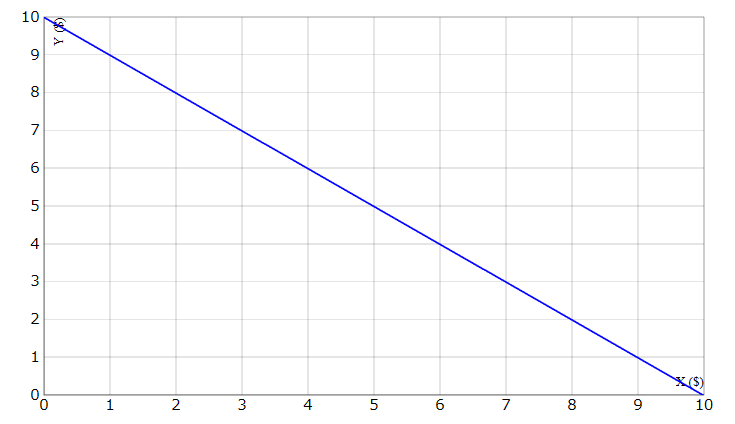

xとyは流動性プール内の仮想通貨ペアそれぞれの枚数です。kは流動性プール毎に決まった値で変わらない定数です。
Constant Sum AMMはステーブルコインに適したAMMなので、ステーブルコインを例に挙げて考えてみましょう。
ステーブルコインAとステーブルコインBの流動性プールがそれぞれ100枚ずつで作られました。
このとき、この流動性プールのConstant Sum AMMの式は次のように表されます。
\(x+y=200\)
この流動性プールでステーブルコインA1枚をステーブルコインBに交換してみましょう。
ステーブルコインAが1枚流動性プールに加わると、AMMの式により、yの値が求まります。
\(101+y=200\)
\(y=99\)
このyの流動性プールの変化分がステーブルコインAをスワップすることによって受け取れるステーブルコインBの枚数なので、1枚になります。(100-99=1)
つまり、Constant Sum AMMでは常に仮想通貨が同じ枚数スワップされ続けることになります。



2枚なら2枚とスワップ、5枚なら5枚とスワップされます。
ステーブルコインは価格がドルで固定されていて価格が変わらず、本来であればこのように常に同じ枚数ずつスワップされるべき仮想通貨なので、Constant Sum AMMはぴったりという訳です。
しかし、実際はステーブルコインの価格はドルに完全に連動する訳ではありません。
ステーブルコインの価格の裏付け理由はいくつかありますが、最もメジャーなステーブルコインUSDCでは、USDCを発行している企業Circleが発行しているUSDCと同等の資産を持っていることが理由です。
2023年3月に米シリコンバレー銀行が経営破綻した際に、Circleはシリコンバレー銀行に33億ドルを預けていたため、USDCの価格が一時的に大きく下がってしまいました。
Coinpost:米サークル、シリコンバレー銀行で33億ドルのUSDC準備金の送金が保留状態に


このようにドルと連動から外れることを「ペグが外れる」「デペグ」と呼んだりします。
シリコンバレー銀行経営破綻の事例では、USDCをCircleで米ドルに戻せない可能性が生まれます。
そうすると、USDCを持っている人は他のステーブルコインに交換しようとするのですが、バイナンス等の仮想通貨取引所ではUSDCを1ドルを下回った価格で売ることになります。



USDCを安く買い付けようとする投資家がいたり、1ドル以下でも良いので手元のUSDCを早く売りたい人がいたりするからです。
こうしてUSDCは一時的に0.9ドル近くまで下がりました。
その後は33億ドルについて問題なくアクセスできると語られたため、すぐにUSDCは価格を戻しました。
話をAMMに戻すと、このようにステーブルコインはペグが外れて急な値崩れが起きる場合もあるということです。
そんな時にConstant Sum AMMでUSDCを必ずUSDT1枚にスワップできる流動性プールがあったらどうなるでしょうか。
すぐにUSDCはUSDTとスワップされ、USDTはプールから枯渇してしまうでしょう。
USDCのペグが外れた場合、それはUSDCの価値が下がっているという紛れもない事実なので、それは分散型取引所の価格にも反映されるべきです。
つまり、Constant Sum AMMだけではステーブルコイン同士の流動性プールのAMMには不十分であることが分かります。



実際にこのConstant Sum AMMを採用している分散型取引所は私が知る限りありません。
②Constant Product AMMとは
Constant Product AMMはステーブルコイン同士以外の仮想通貨のスワップで使われている代表的なAMMです。(イーサリアムとステーブルコインのスワップ等)
Constant Product AMMは直訳すると「定積による価格自動決定システム」です。
このAMMには次のメリット・デメリットがあります。
- 仮想通貨の価格がしっかり動く
- プールが枯渇しない
- ステーブルコインの価格も動く
Constant Product AMMは次の式で表されます。(Constant Sumでkを使ったのでcに変更)
\(xy=c\)
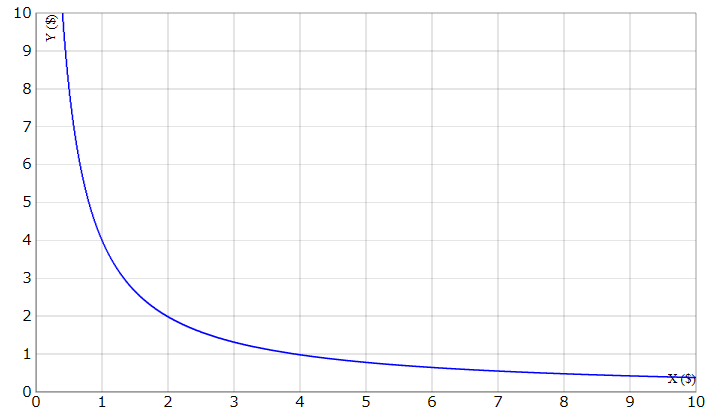

xとyは流動性プール内の仮想通貨ペアそれぞれの枚数です。cは流動性プール毎に決まった値で変わらない定数です。
イーサリアムとUSDCをそれぞれx、yとして価格の動き方を見てみましょう。
流動性プールにUSDCは4000枚、ETHは2枚ありました。
分数取引所内の仮想通貨の価格は単純な割り算できまるので、このときETHの価格は2000USDC/ETHになります。
AMMの式は次のようになります。
\(xy=8000\)
ここでUSDCを1000枚をETHにスワップしてみましょう。USDCのプールが1000枚増えて5000枚になり、x(ETH)の枚数はAMMの式で決定されます。
\(5000x=8000\)
\(x=1.6\)
当初のETHは流動性プールに2枚あったので、差額の0.4枚が今回の1000USDCを1000枚スワップした時の受け取り分となる仕組みです。
価格にすると2500USDC/ETHになります。



スワップする前は2000USDC/ETHだよね?かなり不利な価格でスワップしているような・・・
ここがポイントで、自分のスワップがプールに与える影響が大きいと、自分のスワップにも影響するようになっています。
これをPrice Impact(プライスインパクト)と呼びます。
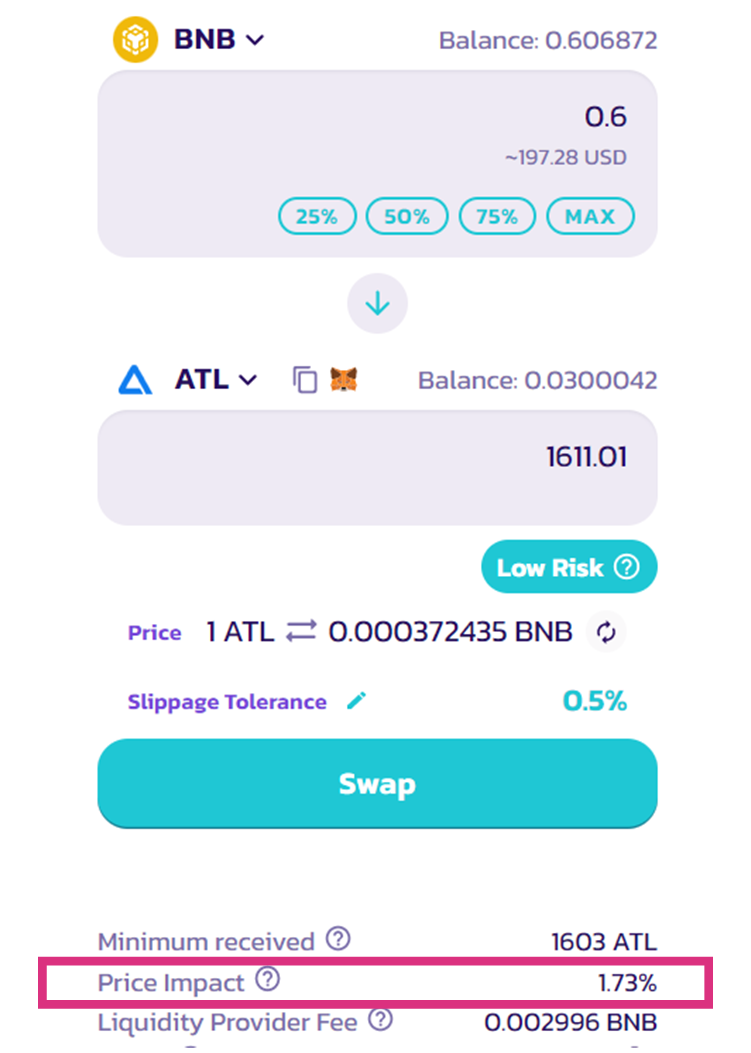

これにより、プールは絶対に枯渇しないようになっています。
もっと大きい例を考えてみましょう。このプールに対して16,000USDCでETHをスワップしてみます。
\(20000x=8000\)
\(x=0.4\)
差額の1.6ETHしか受け取れず、価格にすると10,000USDC/ETHです。
xy=8000は以下のようなグラフになり、ここまで例に挙げた分数型取引所のプール状況をプロットしました。


どれだけプールのUSDCが増えてもETHがゼロになることがないことが分かります。(ゼロに近づくが、ゼロには決してならない)
言い換えると、プールに対してあまりにも大きい数量をスワップすると、Price Impactによりまともにスワップできないということです。



最初の話に戻りますが、ステーブルコイン同士のスワップには適していないことが分かります。
StableSwap AMMとは①②の良いとこ取り


StableSwap AMMは、次の2つのAMMを組み合わせた仕組みになっています。
- Constant Sum AMM(コンスタントサム AMM)
- Constant Product AMM(コンスタントプロダクト AMM)
Constant Sum AMMとConstant Product AMMにはそれぞれ次の問題点がありました。
- Constant Sum AMM:プールが簡単に枯渇する
- Constant Product AMM:ステーブルコインの価格が変化
StableSwap(ステーブルスワップ)はこの2つの問題点を解決したAMMです。
結論、Stable Swap AMMではプールの中身が均衡している状態では仮想通貨の価格が変わりづらくなり、均衡していない状態では価格がしっかり変動するようになります。
ステーブルコイン同士の流動性プールを考えた時、同じくらいの枚数が入っていたら(売り圧買い圧が同じ)、ステーブルコインの価格は変化しづらいという意味です。
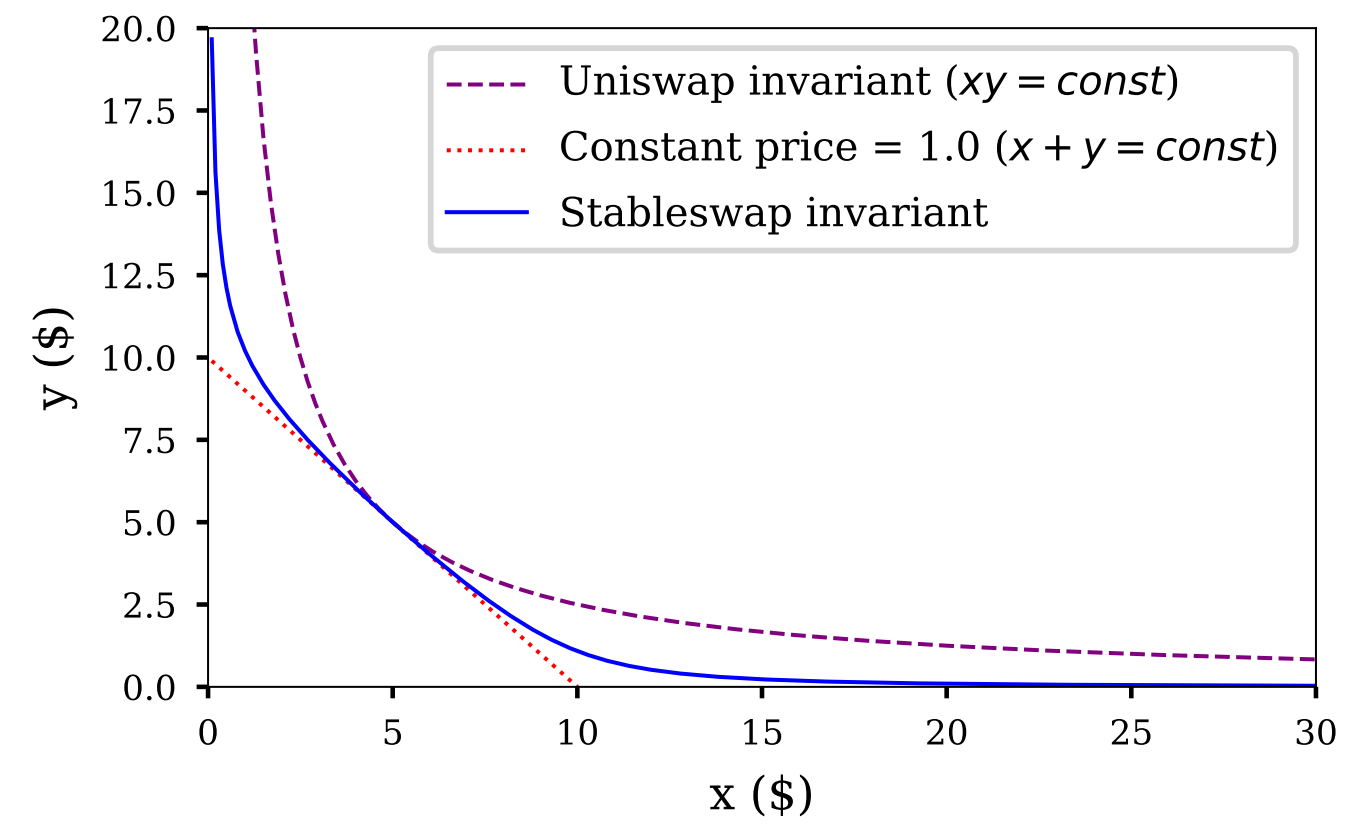

liquidity
- 赤色の点線:Constant Sum AMM
- 灰色の点線:Constant Product AMM
- 青色の実線:StableSwap AMM
StaleSwap AMMの仕組みは次の式で表されます。(2種類のステーブルコインが入った流動性プールの時)
\(γD(x+y)+xy=γD^2+(D/2)^2\)
xとyは流動性プール内の2種類のステーブルコインの枚数を表しています。



スワップによって枚数が変わった流動性プールxの枚数を入れると、yの方がいくら変わるか分かる式になっています。
この式がどうすれば「プールの中身が均衡している状態では価格が変わりづらくなり、均衡していない状態では価格がしっかり変動する」ことを表せるのかを意識しながら追ってみて下さい。
Constant Sum AMMとConstant Product AMMをそれぞれ次の式で表します。
\(x+y=D\)
\(xy=(D/2)^2\)
Dは流動性プール内の仮想通貨xとyの価格が同じになっているときのxとyの枚数の合計で、最初に流動性プールを作った時に決めてしまいます。
x+yはDと表すことができますね。
次に、xyをDを使って表してみましょう。Dをプール内の仮想通貨種類の数である2で割って、その2個でべき乗するとxyになります。
この2つの式をそのまま足します。
\(x+y+xy=D+(D/2)^2\)
左辺と右辺に2つのAMMの要素が組み合わさりました。ここでConstant Sum AMMの要素にだけ、γ(ガンマ)を掛けます。
\(γ(x+y)+xy=γD+(D/2)^2\)
γ(ガンマ)を入れることにより、γがゼロの時にこの式は完全にConstant Product AMMの式になり、逆にγが十分に大きい時にこの式はConstant Sum AMMの式になるようになりました。
あとはこのγの値がプールの中身が均衡しているときは大きくなるように、プールの中身が均衡していないときは小さくなるように設定すれば、最初に目指していたAMMの仕組みを式で表せます。
プールの中身が均衡している状態では価格が変わりづらくなり、均衡していない状態では価格が変わりやすくなる。
γは次のように定めます。
\(γ=A\frac{xy}{(D/2)^2}\)
Aという文字が新しく出てきましたが、こちらは後で考えましょう。
Aの右の分数の部分は完全にプールの中身が均衡していると1になり、均衡から外れるとどんどん小さくなります。
以下の表で確認してみましょう。
| x | y | xy | D | \(\frac{xy}{(D/2)^2}\) | 均衡 |
|---|---|---|---|---|---|
| 100 | 100 | 10000 | 200 | 1 | ◯ |
| 99 | 101 | 9999 | 200 | 0.999 | ◯ |
| 90 | 110 | 9900 | 200 | 0.990 | ◯ |
| 30 | 170 | 5100 | 200 | 0.510 | × |
| 1 | 199 | 199 | 200 | 0.019 | × |
このようにxとyの枚数に差が出てきて均衡しなくなると、分数の値はどんどん小さくなります。
これでほとんどγ(ガンマ)の役割を表せましたが、最後にAの値について考えましょう。
Aの値は分散型取引所のコミュニティ(DAO)の中の投票で決まります。
分散型取引所は特定の管理者によって仕組みが全て決まるのではなく、重要な方針はコミュニティの投票で決まります。



だから「分散型」取引所となっている訳ですね。
例えば、あるステーブルコイン同士の流動性プールで、両方のコインが絶対に裏付けとなっている資産(ペグ)が外れることがない安全なコインである場合、Aの値はとてつもなく大きくすれば良いということです。
実際にはそんなステーブルコインはないので、コミュニティでちゃんと決めます。
例えば、A=10のときの先程の表でγ(ガンマ)を見てみましょう。
| x | y | xy | D | \(\frac{xy}{(D/2)^2}\) | γ |
|---|---|---|---|---|---|
| 100 | 100 | 10000 | 200 | 1 | 10 |
| 99 | 101 | 9999 | 200 | 0.999 | 9.99 |
| 90 | 110 | 9900 | 200 | 0.990 | 9.90 |
| 30 | 170 | 5100 | 200 | 0.510 | 5.10 |
| 1 | 199 | 199 | 200 | 0.019 | 0.19 |
均衡しているときγは10になるので、Constant Sum AMMの影響が大きくなります。
表の一番下の例の場合、均衡していないためγの値は0.19になっており、Constant Sum Productの影響が大きくなります。
このようにγが均衡状態を表すことで、下の式は「プールの中身が均衡している状態では価格が変わりづらくなり、均衡していない状態では価格が変わりやすくなる」を表す訳ですね。
\(γ(x+y)+xy=γD+(D/2)^2\)



最初に見た式とまだちょっと違くない?
この後、最後にConstant Sum AMMの要素にだけDを掛ける必要があります。
\(γD(x+y)+xy=γD^2+(D/2)^2\)
Dを掛けると最初に見たStableSwap AMMの形になる訳ですね。
Dを掛ける理由は少し複雑です。
ステーブルコインをスワップする際のStableSwap AMMですが、このルールはプールの中身がステーブルコイン2種類ではなく、3種類・4種類とどんなプール内の種類数でも対応できる式になっています。
StableSwap AMMの文献を出しているCurveの分散型取引所には3種類・4種類のステーブルコインが入った流動性プールが実際にあるからです。



このことを考えると、Dを掛ける理由が分かります。
γ(ガンマ)の値は次のように計算されました。
\(γ=A\frac{xy}{(D/2)^2}\)
流動性プール内のステーブルコインの種類の数が3個の場合、この式は次のようになります。
\(γ=A\frac{xyz}{(D/3)^3}\)
流動性プール内のステーブルコインの種類の数がn個の場合、この式は次のようになります。
\(γ=A\frac{xy・・}{(D/n)^n}\)
ここで問題になるのが、γの分母にDのn乗が入ってしまうことです。
γの値はConstant Sum AMMの影響が強い式にするか、Constant Product AMMの影響が強い式にするかに変えるためのパラメーターのような役割でした。
そこでγにはDのn-1乗を掛けるようにします。こうすることで、γの分母は必ずDになります。nが入っていないので、γは流動性プール内の仮想通貨の個数がいくつでも対応できます。
だから先程のステーブルコイン2種類の例では、Dの2-1乗としてDを掛けたという訳です。
Constant Sum AMM、Constant Product AMM、StableSwap AMMをそれぞれグラフに示すと次のようになります。
- 赤色の点線:Constant Sum AMM
- 灰色の点線:Constant Product AMM
- 青色の実線:StableSwap AMM


liquidity



グラフで見るとStableSwap AMMがConstant SumとConstant Productの良いところ取りをした仕組みであることがよく分かります。
StableSwap AMMの解説は以上になります。
StableSwapに数字を入れてグラフを作る


ステーブルコインA・Bがそれぞれ100万枚ずつ提供されている流動性プールのStableSwap AMMをグラフにしてみました。
StableSwap AMMの式は次のようになります。


- Dは100万枚+100万枚=200万で固定しています。
- Aの値を動かすと、直線に見える部分を伸ばしたり、短くしたりできます。
マイナスの値もグラフで表現されてしまっていますが、定義する方法が分からずご容赦下さい。


liquidity

ご覧いただきありがとうございました。
本記事に関するご質問・ご感想はコメント欄か下記のお問い合わせページ・XのDMよりお送り下さい。丁寧に回答させていただきます。
メールアドレスはこちら:contact@pandacrypto.xsrv.jp

ご覧いただきありがとうございました。
本記事に関するご質問・ご感想はコメント欄か下記のお問い合わせページ・XのDMよりお送り下さい。丁寧に回答させていただきます。
メールアドレスはこちら:contact@pandacrypto.xsrv.jp
仮想通貨に関する注意喚起



仮想通貨に関する法令・注意喚起について知りたい方は、以下の関連ページを一読することをオススメします。
| 金融庁 | 暗号資産の利用者のみなさまへ |
| 警察庁 | 暗号資産(仮想通貨)に関するトラブルにご注意ください! |
| 消費者庁 | 投資などのお金に関するトラブルや悪質商法について |
| 国税庁 | 仮想通貨の税務上の取扱い-現状と課題- |
| 政府広報オンライン | 暗号資産の「必ずもうかる」に要注意! |
| 日本暗号資産取引業協会 | 暗号資産に関するトラブルにご注意ください! |
| 国民生活センター | 暗号資産に関する消費者トラブル |






コメント