集中流動性(UniswapV3)のインパーマネントロスとは？仕組み・計算方法

2025年11月3日

さとう

※本記事は「通常のインパーマネントロス」を理解している方向けです。

この記事から分かること

集中流動性のインパーマネントロス
インパーマネントロス損失早見表
損失シミュレーションツール

この記事を書いた人

ぱんだくりぷと運営者”さとう”
米国公認会計士（WA州）
仮想通貨投資歴5年
公式白書のリサーチ・運営者自身の実体験・その他の信頼できる情報源を基に記事を作成
本質が分かるイラストや丁寧な解説であなたのクリプトに関する疑問を解決します
X(旧ツイッター)はこちら
詳しい運営者情報はこちら

※本記事へのコメント・質問等は私のX（旧ツイッター）にDMで送っていただいても大丈夫です。丁寧に回答させていただきます。

分散型取引所の集中流動性（Concentrated Liquidity）は、2021年5月5日にユニスワップのV2がV3にアップデートされ初めて導入されました。

以降「パンケーキスワップ」や「Cetus」といった代表的な分散型取引所ほぼ全てで「集中流動性」は導入されており、現在の流動性のスタンダードな仕組みになっています。

集中流動性では、事前に流動性を提供する「価格範囲」を設定する必要があり、その期間に現在価格が該当している時だけ手数料報酬をもらえます。

これまで0から無限の価格範囲の全ての流動性に対して手数料報酬が発生していましたが、集中流動性では価格範囲内の該当するポジションにしか発生しないため、利率が高くなります。

さとう

集中流動性導入の目的は「資本効率性を高めること」です。

不要な流動性の提供を防ぎ、流動性提供者の利率を高めるだけでなく、仮想通貨を「PoSステーキング」など本来のあるべき場所に戻すことでセキュリティを高めることにも繋がる訳です。

資本効率性と年間利率が高まる一方、「インパーマネントロス」による損失リスクも高まるため、価格範囲に対応する損失リスクを把握しておく必要があります。

※インパーマネントロス：Impermanent Loss（一時的損失、変動損失）

集中流動性では上限価格または下限価格に達すると片方のトークンがもう片方のトークンに全て置き換わり、インパーマネントロスが最大になります。

さとう

BTCとUSDTを流動性として提供するときの、下限と上限価格に対応するインパーマネントロスの発生率は次の表になります。

スクロールできます

下限価格 (BTC/USDT)	現在価格 (BTC/USDT)	上限価格 (BTC/USDT)	インパロス (通常)	インパロス (集中流動性)	損失倍率 (通常vs集中)
95,238	100,000	105,000	0.03%	1.23%	41.5倍
90,909	100,000	110,000	0.11%	2.44%	21.5倍
83,333	100,000	120,000	0.41%	4.75%	11.5倍
66,667	100,000	150,000	2.02%	11.01%	5.4倍
50,000	100,000	200,000	5.72%	19.53%	3.4倍
33,333	100,000	300,000	13.40%	31.70%	2.4倍
25,000	100,000	400,000	20.00%	40.00%	2.0倍

集中流動性インパーマネントロス早見表

※この表はインパーマネントロスのイメージを出来るだけ分かりやすくするため、「現在価格と下限価格」「現在価格と上限価格」の比率を同じにしています（現在価格/上限価格＝下限価格/上限価格）。上限価格まで価格が変化した場合と、下限価格まで価格が変化した場合のインパロスが同じになるからです。

一番上の行で例えると、現在価格が100,000USDT/BTCのときに、下限価格を「95,238USDT」、上限価格を「105,000」で提供した場合、価格が上限価格または下限価格まで変化した場合のインパーマネントロスの発生割合を示します。

価格範囲の設定がない通常の流動性（V3以前）であれば0.03%ですが、集中流動性では41.5倍の1.23%のインパーマネントロスが発生します。

この時点で流動性提供を解除すると、流動性を提供していなかった場合の資産額×1.23%の損失が確定するため、この1.23%分より高い利回りを稼いでいるかどうかが運用成功の判断基準になる訳です。

5,000ドル程度の価格変化はBTCではすぐに発生します。

さとう

価格範囲を狭く設定し過ぎると、高い利回りを稼いでもILで相殺されたり損失が上回る可能性があることを押さえておきましょう。

本記事の以降の内容は、集中流動性のインパーマネントロス発生の仕組みや上表の作成方法を解説しています。

本記事の参考文献

https://uniswapv3book.co m
https://uniswap.org/whitepaper-v3.pdf
Peteris Erins “Impermanent Loss in Uniswap V3“

集中流動性のインパーマネントロスの仕組み

通常の流動性（Uniswap V3前）のおさらい

通常の流動性提供（UniswapV2）の流動性の仕組みをおさらいします。

通常に流動性では、次の式に従って流動性の枚数や仮想通貨の価格が変化していました。

\(xy=k\)

流動性が新規で提供されたり、削除されたりする時のみkが再計算され、流動性提供プールのペアxとyの枚数は常にxy=kのグラフに従って変化する仕組みです。

※xとyの定積AMM（Constant Product AMM）

集中流動性の流動性提供の計算式

集中流動性のインパーマネントロスの前に、集中流動性の流動性提供の計算式を先に理解しておきましょう。

集中流動性は同じ価値のペアで流動性を提供する必要がなく、価格範囲の設定次第では片方のトークンだけを流動性として提供することもできます。

集中流動性（Uniswap V3以降）では、次のxy=kをベースにした式（kをL二乗で表現しただけ）を変形していくことで、各流動性提供者個別の集中流動性の式を導くことができます。

\(xy=L^2\)

さとう

価格をPとすると、Pは次のように表せます。

\(P=\frac{y}{x}\)

xとyはそれぞれLとPを使って次のように表せます。

①：\(xy=L^2\)

②：\(y=Px\)

上記の2式より、

\(x=\frac{L}{\sqrt{P}}\)

\(y=L\sqrt{P}\)

この式は、ある価格区間に含まれる全ての個別の流動性の傾きL（後述）の合計と、流動性の合計x・yと、それらによって定義される価格Pの関係を表した式です。

しかし、あなたが行う集中流動性は自身で決めた価格範囲に従い、あなた特有の流動性ポジションの変化をするため、この式であなたの流動性は一切定義されません。

集中流動性の提供では価格範囲を設定し、上限または下限に達すると片方のトークンだけが残るため、この仕様を式に反映させて、あなただけの集中流動性の関係式を導く必要があります。

今回は例として、集中流動性で提供する流動性「BTC＆USDT」の枚数は「BTCがx」、「USDTがy」で考えます。BTCのUSDT建価格がPです。

提供する流動性の下限価格をPb、上限価格をPaとします。

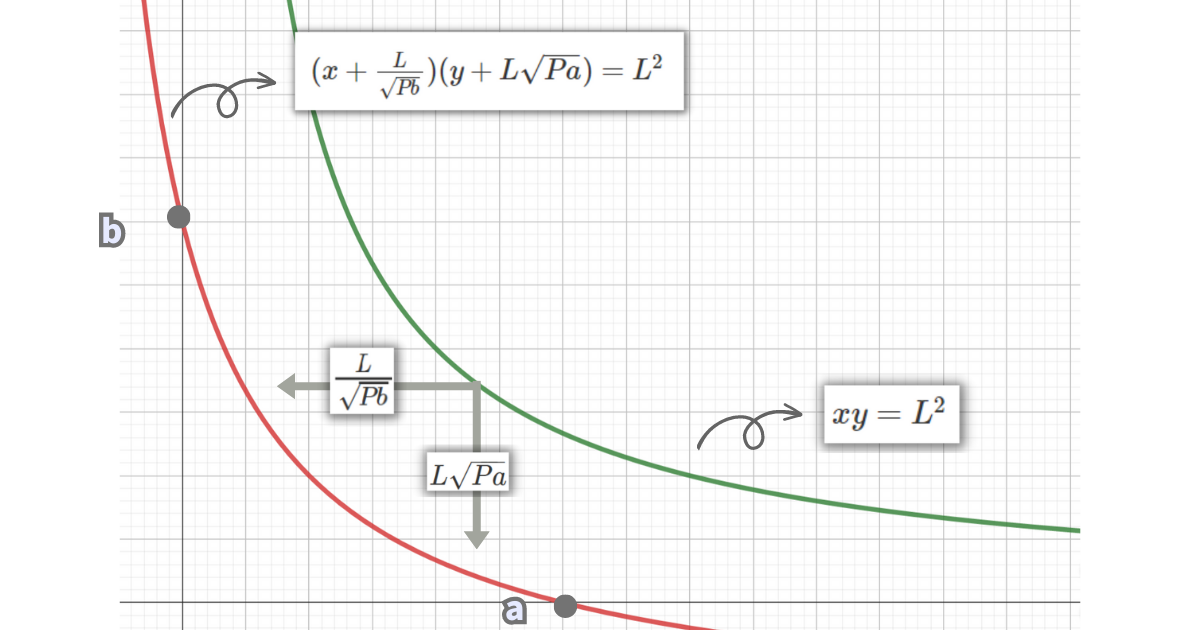
集中流動性は価格範囲を設定し、上限または下限価格で片方のトークンだけが残る仕様でしたが、これは次のようなグラフを指します。

\(xy=L^2\)のグラフを－x方向に\(\frac{L}{\sqrt{Pb}}\)だけ平行移動する
\(xy=L^2\)のグラフを－y方向に\(L\sqrt{Pa}\)だけ平行移動する

平行移動させたグラフとその式が次の通りです。

\((x+\frac{L}{\sqrt{Pb}})(y+L\sqrt{Pa})=L^2\)

ここまでの式を使い、次の条件で10,000USDTを流動性提供した時のBTCの提供枚数を求めてみます。

提供する流動性ペア：BTC&USDT
現在のBTCの価格：10,000USDT/BTC
流動性の上限価格：14,400USDT/BTC
流動性の下限価格：8,100USDT/BTC
提供するUSDTの枚数：10,000USDT
提供するBTCの枚数：？（ここを求める）

平行移動した式のyに10,000を入れれば良さそうですが、まだLが分かっておらず対応するxを算出できません。

※平行移動前の式はあくまでも平行移動後の式を求めるためのもので、別の式なので関係ない。Lの値も平行移動前と平行移動後では基本的に異なる。（流動性が複数存在する場合）

そこで、集中流動性で成り立つ次の2つの関係式で考えます。

\(\Delta y=L・\Delta\sqrt{P}\)

\(\Delta x=L・\Delta\frac{1}{\sqrt{P}}\)

これらは平行移動前の式から導き出せる式を変化量で定義し直しただけの式で、x・y・Pの変化の関係を表します。この式の証明は下のボックスを開くと表示されます。

上記2式の証明過程【開けます】

\(\Delta Y=L・\Delta\sqrt{P}\)

\(\sqrt{xy}=\frac{y_{1}-y_{0}}{\sqrt{P_{1}}-\sqrt{P_{0}}}\)

\(\sqrt{xy}(\sqrt{P_{1}}-\sqrt{P_{0}})=y_{1}-y_{0}\)

\(\sqrt{xy}(\sqrt{\frac{y_{1}}{x_{1}}}-\sqrt{\frac{y_{0}}{x_{0}}})=y_{1}-y_{0}\)

Virtual Curve上では、\(\sqrt{x_{1}y_{1}}=\sqrt{x_{0}y_{0}}=\sqrt{xy}=L\)のため、

\(\sqrt{\frac{x_{1}y_{1}y_{1}}{x_{1}}}-\sqrt{\frac{x_{0}y_{0}y_{0}}{x_{0}}}=y_{1}-y_{0}\)

\(\sqrt{y_{1}^2}-\sqrt{y_{0}^2}=y_{1}-y_{0}\)

\(y_{1}-y_{0}=y_{1}-y_{0}\)

Δxについても同様です。

この流動性と価格変化量の関係式は、平行移動前の式から導かれたものですが、この式は平行移動後の実際の集中流動性の式においても同じように適用でき、集中流動性における流動性の枚数変化と価格変化の関係性も表します。

ちなみに、ユニスワップ公式文献では平行移動前の式は実際の流動性の枚数関係を表さない「Virtual Curve」と呼ばれ、平行移動後の式は「Real Curve」と呼ばれます。

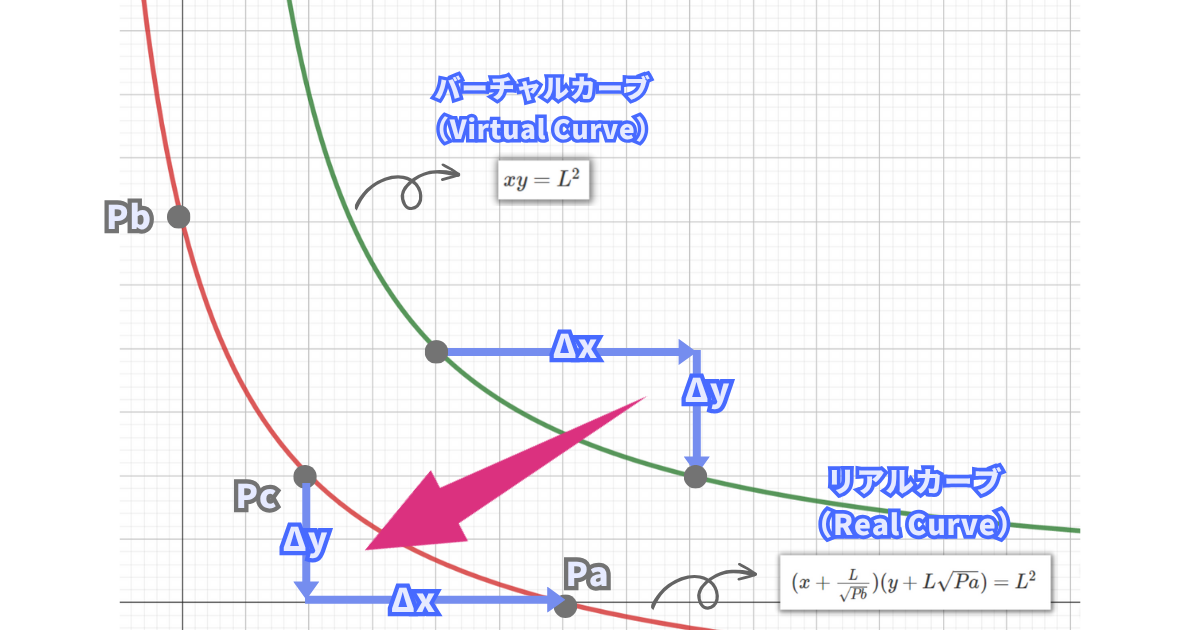
つまり、平行移動後の集中流動性の式は実際の流動性の枚数関係を表しますが、下限価格から上限価格までの流動性の枚数変化の仕方はxy=k（通常の流動性モデル、集中流動性におけるVirtual Curve）と同じになります。

集中流動性では価格範囲ごとに「独立したミニ定積AMM（xy=k）」が存在しているということです。

つまり、集中流動性のグラフにおける変化量の関係式は次のようになります。

\(\Delta x=L(\frac{1}{\sqrt{Pc}}-\frac{1}{\sqrt{Pb}})\)

\(\Delta y=L(\sqrt{Pc}－\sqrt{Pa})\)

例題の値を当てはめると次のようになります。

\(\Delta x=L(\frac{1}{\sqrt{10000}}-\frac{1}{\sqrt{14400}})\)

\(10000=L(\sqrt{10000}－\sqrt{8100})\)

最初にLが1000であることが分かり、BTCの提供枚数（Δx）=1.6666…であることが分かります。

今回の例では設定した価格範囲で現在価格は下限価格に寄っているため、BTCの価格が上がったときに利用されやすい流動性の提供方法といえます。

※BTCの価格が上がった時＝BTCが流動性から少なくなったときであり、資本効率性の観点ではより多くのBTCをプールが必要としています。

下の集中流動性のシミュレーションを使って例題の状況を入力すると（トークンの提供枚数10000枚）、同じようにBTCの提供枚数は1.6666で出力されるはずです。

集中流動性 IL計算ツール

①～⑤まで入力して「計算開始」を押すと、対応する流動性枚数とインパーマネントロスが計算されます。価格は A/B（1 B あたり A） で入力してください。例：USDT/BTC = 10000

① 提供するトークンA枚数（A）：

② 下限価格（A/B）：

③ 上限価格（A/B）：

④ 現在価格（A/B）：

⑤ 将来価格（A/B）：

集中流動性のインパーマネントロス計算

先程の例を使って、BTC価格が現在価格10,000USDT/BTCから、12,000USDT/BTCになった時インパーマネントロスがどれくらい発生するか具体的に計算してみましょう。

※上のシミュレーションツールの例でもある。

将来価格をPfとすると、次のようにΔxとΔyの値を求められます。

\(\Delta x=L(\frac{1}{\sqrt{Pf}}-\frac{1}{\sqrt{Pb}})\)

\(\Delta y=L(\sqrt{Pf}－\sqrt{Pa})\)

Pf：将来価格（価格変化後）

\(\Delta x=1000(\frac{1}{\sqrt{12000}}-\frac{1}{\sqrt{14400}})\)

\(\Delta y=1000(\sqrt{12000}－\sqrt{8100})\)

x=0.79537…

y=19,544…

流動性を提供した時にLが1000であることが分かっているので、今回は簡単に計算できました。

将来価格時点のポジションの合計金額は合計金額は「0.79537×12000+19544=29,088ドル」となります。

流動性を提供していなかった場合は「1.66666×12000+10000=30,000ドル」となります。

従ってインパーマネントロスの割合は912/30000=約3.04%です。

さとう

シミュレーションツールで同じ条件を入れると、3.04%になるはずです。

設定した価格範囲が狭ければ狭いほどインパーマネントロスは大きくなり、広くすれば従来のV2のインパーマネントロスの発生に近づきます。

価格範囲毎のインパーマネントロス目安

集中流動性における価格範囲毎のインパーマネントロスの目安を考えてみましょう。

発生するインパーマネントロスの割合は次の式で計算できます。

\(変動損失=\frac{価格変化後の流動性金額-ガチホ時の金額}{ガチホ時の金額}\)

流動性を提供した時点の流動性金額の合計をV₀、価格変化後の提供した流動性の金額をV₁、流動性を提供していなかった場合の金額をV_heldとします。

このときV₀は、現在価格Pを使って次のように表せます。

\begin{eqnarray} V_{ 0 }&＝&y+xP\\ \end{eqnarray}

xは\(x=L(\frac{1}{\sqrt{P}}-\frac{1}{\sqrt{Pb}})\)、yは\(y=L(\sqrt{P}－\sqrt{Pa})\)なので、V₀はさらに次のように表せます。

\begin{eqnarray} V_{ 0 }&＝&y+xP\\ &＝&L(\sqrt{P}－\sqrt{Pa})+LP(\frac{1}{\sqrt{P}}-\frac{1}{\sqrt{Pb}})\\ &＝&L(\sqrt{P}－\sqrt{Pa})+LP(\frac{1}{\sqrt{P}}-\frac{1}{\sqrt{Pb}})\\ &＝&L(\sqrt{P}－\sqrt{Pa})+L(\sqrt{P}-\frac{P}{\sqrt{Pb}})\\ &＝&2L\sqrt{P}－L(\sqrt{Pa}-\frac{P}{\sqrt{Pb}}) \end{eqnarray}

V0の式はL・P・Pa・Pbの4つで構成される式で、P以外の3つは流動性を提供する時に決まった値で固定です。

つまり、Pを将来価格に置き換えるだけでV0の式はV1の式になります。

将来価格を現在価格Pをk倍したPkとすると、V₁は次のようになります。

\begin{eqnarray} V_{ 1 }＝2L\sqrt{Pk}－L(\sqrt{Pa}-\frac{Pk}{\sqrt{Pb}}) \end{eqnarray}

V_heldは、Pkを使って次のように表せます。

\begin{eqnarray} V_{ held }&＝&y+xPk\\ &＝&L(\sqrt{P}－\sqrt{Pa})+LPk(\frac{1}{\sqrt{Pk}}-\frac{1}{\sqrt{Pb}})\\ &＝&L\sqrt{P}(1+k)-L(\sqrt{Pa}+\frac{Pk}{\sqrt{Pb}})\\ \end{eqnarray}

価格範囲PaからPbにおける、現在価格からk倍の将来価格時点でのインパーマネントロスの割合をIL_a,b(k)とすると、次のように表せます。

\begin{eqnarray} IL_{ a,b }(k)&＝&\frac{V_{ 1 }-V_{ held }}{V_{ held }}\\ &＝&\frac{2L\sqrt{Pk}-L\sqrt{P}(1+k)}{L\sqrt{P}(1+k)-L(\sqrt{Pa}+\frac{Pk}{\sqrt{Pb}})}\\ &＝&\frac{2\sqrt{k}-1-k}{1+k-\sqrt{\frac{Pa}{P}}-k\sqrt{\frac{P}{Pb}}} \end{eqnarray}

通常（V2）のインパーマネントロスの割合をIL(k)すると、IL(k)は\(\frac{2\sqrt{k}-1-k}{1+k}\)で表すことができるので、この値でIL_a,b(k)の計算結果を無理矢理くくると次のようになります。

\begin{eqnarray} IL_{ a,b }(k)&＝&IL(k)・\Bigg(\frac{1}{1-\frac{\sqrt{\frac{Pa}{P}}+k\sqrt{\frac{P}{Pb}}}{1+k}}\Bigg) \end{eqnarray}

現在価格P、レンジ下限Pa、レンジ上限Pbを入れて将来価格が何倍になったかを表すkを入れると、集中流動性のインパーマネントロスが通常のインパーマネントロスに対して何倍か分かる式が完成しました。

さらに分かりやすくするために、上限価格と下限価格時点で同じ割合のインパーマネントロスが発生するシチュエーションに限定してみます。

そこで、次の2つの式を満たすようなnを決めます。

\begin{eqnarray} \frac{Pa}{P}=\frac{1}{n}、 \frac{P}{Pb}=\frac{1}{n} \end{eqnarray}

この2つの式をIL_a,b(k)の式に代入すると、次の式が得られます。

\begin{eqnarray} IL_{ a,b }(k)&＝&IL(k)・\Bigg(\frac{1}{1-\frac{\sqrt{\frac{Pa}{P}}+k\sqrt{\frac{P}{Pb}}}{1+k}}\Bigg)\\ &＝&IL(k)・\Bigg(\frac{1}{1-\frac{\sqrt{\frac{1}{n}}+k\sqrt{\frac{1}{n}}}{1+k}}\Bigg)\\ &＝&IL(k)・\Bigg(\frac{1}{1-\frac{(1+k)\sqrt\frac{1}{n}}{1+k}}\Bigg)\\ &＝&IL(k)・\frac{1}{1-\frac{1}{\sqrt{n}}} \end{eqnarray}

この式より、等間隔（比率）で価格範囲を設定したとき、集中流動性のインパーマネントロスが通常と比べて何倍大きいかをnによって示せるようになりました。

\(f(n)=\frac{1}{1-\frac{1}{\sqrt{n}}}\)（n>1）のグラフとnの値毎の倍率のテーブルは次のようになります。

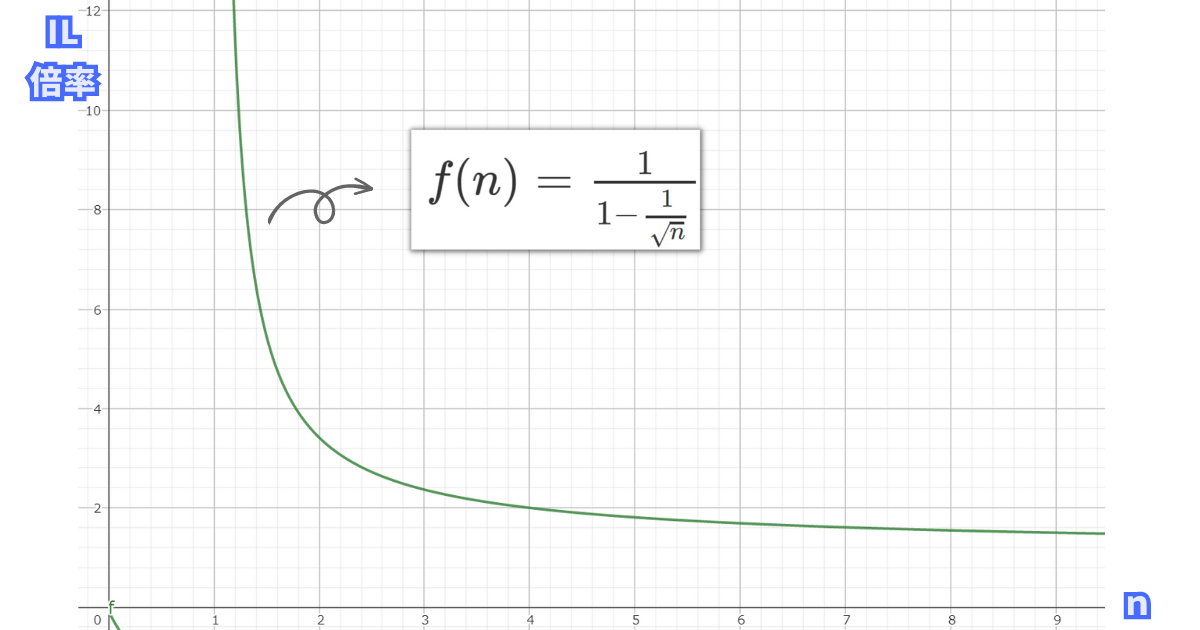
このnの式をもとに、現在価格100,000USDT/BTCで各nにおけるインパーマネントロスの発生割合をまとめると、冒頭で作成した表が完成します。

スクロールできます

nの値	下限価格 (BTC/USDT)	現在価格 (BTC/USDT)	上限価格 (BTC/USDT)	インパロス (通常)	インパロス (集中流動性)	損失倍率 (通常vs集中)
1.05	95,238	100,000	105,000	0.03%	1.23%	41.5倍
1.10	90,909	100,000	110,000	0.11%	2.44%	21.5倍
1.20	83,333	100,000	120,000	0.41%	4.75%	11.5倍
1.50	66,667	100,000	150,000	2.02%	11.01%	5.4倍
2.00	50,000	100,000	200,000	5.72%	19.53%	3.4倍
3.00	33,333	100,000	300,000	13.40%	31.70%	2.4倍
4.00	25,000	100,000	400,000	20.00%	40.00%	2.0倍

さとう

分散型取引所にもよりますが、初期設定だとn=2.0の等比で価格範囲が設定されている所が多い印象です。

【補足】集中流動性はTickで各流動性を管理する

ここまで各個人の集中流動性提供で発生するインパーマネントロスに着目してきましたが、ここから補足としてスワップが発生してから各個人の流動性ポジションが変化する過程を詳しく解説します。

集中流動性のもとでは、各個人が設定した独自の様々な価格範囲の流動性が大量に配置されるため、これを上手く管理するための概念としてTick（ティック）を用いています。

Tickは「ある2つの価格間の範囲」を表す概念で、Tickの区切れ目は次の式で計算されます。

\[ P = 1.0001^{t} \]

※tはtick indexと呼ばれる正の整数

1.0001倍毎にTickの区切れ目があり、その間隔それぞれが1つのTickとなります。

さとう

この1つのTickそれぞれにVirtual Curveが設定されます。

しかし、流動性を構成するペアによってはあまりにも価格変動が大きく、1,0001倍毎にTickの区切りを設定する意味がない場合もあるため、実際は各ペア毎に「Tick Spacing」を定義し、数十から数百のTickをひとまとまりにします。

例えばユニスワップV3ではこのTick Spacing毎にスワップ手数料が設定される仕組みで、価格変化がほぼないステーブルコインペアなら最小のTick Spacingが設定され、ミームコインを含めば大きく設定されます。

Tick spacing	手数料率	ペア例
1	0.01%	USDC＆USDT
6	0.03%	ETH＆LINK
10	0.05%	ETH＆USDC
200	1.00%	ETH＆GMX

参照：Uniswap “What is a tick when providing liquidity?“

Tick Spacingが細かいほど、特定の価格範囲に絞った流動性の集中がより実現しやすくなります。

従って、米ドルステーブルコイン同士のスワップの場合、ユーザーは1ドル同士のスワップを望むため、Tick Spacingを狭くして1ドル周辺に流動性を集中させます。

流動性提供側の観点で考えると、インパーマネントロス発生のリスクがなく、手数料報酬を多く必要とせずに流動性を提供するインセンティブがあるため、スワップ手数料率は低く設定されます。

集中流動性では、このTick1つ1つにVirtual Curve（xy=L^2）があり、LはそのTickに該当するReal Curveの流動性の合計を表しています。

例えば、微量のスワップが発生して１つTick内に留まる小さな価格変化が起きた場合、次のように各個人の流動性のポジションは変化します。

スワップが発生する
Virtual Curveでx・y・Pが変化
各LPにx・yの変化を配分

まずはVirtual Curve式を用いてスワップによるΔx・Δy・ΔPを算出していきます。

\[ \Delta x = L\left(\frac{1}{\sqrt{P_{\text{変化後価格}}}}-\frac{1}{\sqrt{P_{\text{現在価格}}}}\right) \\ = L\left(\frac{\sqrt{P_{\text{現在価格}}}-\sqrt{P_{\text{変化後価格}}}}{\sqrt{P_{\text{変化後価格}}}\sqrt{P_{\text{現在価格}}}}\right) \] \[ \Delta y = L\left(\sqrt{P_{\text{変化後価格}}}-\sqrt{P_{\text{現在価格}}}\right) \]

Lは現在のTick内においてアクティブな流動性の合計となっており、現在価格は分かっているため、スワップによるΔxが入力されると、Δyとスワップ後の価格Pが計算できます。

これによりスワップによるこのTick区間の全体のx・y・Pの変化が計算できました。ここから、各Real Curve（各個人の流動性）への影響も計算できます。

Virtual CurveとReal Curveは平行移動しただけで同じ傾きのため、Virtual Curveにおける枚数変化の比率とReal Curveにおける枚数変化の比率は同じになります。

従って、TickのVirtual curveにおけるΔxとΔyを各個人Real CurveのL_iで比例配分すると、各個人の流動性ポジションの変化Δx_iとΔy_iが計算されます。

\[ \Delta x_i = \frac{L_i}{L_{\text{合計}}} \, \Delta x \] \[ \Delta y_i = \frac{L_i}{L_{\text{合計}}} \, \Delta y \]

このように、集中流動性ではTickで価格を区分けし、各Tick毎のVirtual Curveと、そのVirtual Curveから枝分かれしたReal Curveで各個人の流動性ポジションを計算・管理している訳です。

まとめ：リスクを理解して価格範囲を決めよう

本記事のまとめは以下の通りです。

集中流動性では価格範囲を設定する
価格範囲を狭くすると利率は高くなる
価格範囲を狭くするとILが大きくなる
価格範囲を広くすると利率は低くなる
価格範囲を広くするとILが小さくなる

ユニスワップV3が集中流動性において重要視する「資本効率」であり、それに従って自分で頻繁に流動性を解除して再配置して資本効率性を高める時間がある方に、特に集中流動性は適しているといえます。

さとう

難しい方は、次の方法で流動性を提供するのがオススメです。

価格変動がないステーブル同士で運用する
利率は諦めて価格を広く設定する
V2流動性プールで運用する
流動性のリポジションを代行させる

「パンケーキスワップ」で上記の流動性マイニング（ステーキング）を行う方法は、下の記事で解説しています。

パンケーキスワップの関連記事はこちら
使い方・始め方のまとめ	スワップのやり方
ステーキングのやり方	草コインの買い方
ポジションマネージャー	メタマスクを接続できない
シンプルステーキング	報酬の収穫タイミング
儲け方・手数料負けしない方法	V3とV2の違い

ユニスワップの関連記事はこちら
スワップのやり方	ステーキングのやり方
V2インパーマネントロス	ユニスワップV3とV2の違い
V3インパーマネントロス	プライスインパクトとは