この記事から分かること
- PancakeSwapV3とV2の違い
- PancakeSwapV3の集中流動性とは
- PancakeSwap Infinityとは
- PancakeSwapとUniswapの違い
※本記事へのコメント・質問等は私のX(旧ツイッター)にDMで送っていただいても大丈夫です。丁寧に回答させていただきます。
分散型取引所パンケーキスワップ(PancakeSwap)は、2023年4月にバージョン3.0であるV3をリリースしました。
パンケーキスワップV3はユニスワップV3をベースに開発されており、「資本効率性」を高めるために「集中流動性」と呼ばれる従来の流動性提供とはまったく異なる仕組みを採用している点が特徴です。
 さとう
さとうパンケーキスワップV2とV3の比較表は次の通りです。
| 比較項目 | V2 | V3 |
|---|---|---|
| リリース時期 | 2020年9月 | 2023年4月 |
| AMMの仕組み | 定積(xy=k) | 集中流動性 |
| スワップ手数料 | 一律0.25% | 選択式 |
| プロトコル手数料 | スワップ手数料から約33%徴収 | スワップ手数料から約33%徴収 |
| 流動性提供範囲 | 一律0~∞ | 自分で設定する |
| 流動性提供利率 | 安定するが低い | 安定しないが高い |
| インパロス | あり | V2の数倍~数十倍 |
| プライスインパクト | 起きやすい | 起きにくい |
| スリッページ | 起きやすい | 起きにくい |
パンケーキスワップ V2 &V3 比較表
パンケーキスワップV3で「スワップ」を行うメリット・デメリットは次の通りです。
- スワップ銘柄により手数料が変わる
- プライスインパクトが発生しづらい
パンケーキスワップV3で「流動性提供」を行うメリット・デメリットは次の通りです。
- もらえる手数料報酬が増える
- 手数料が0になるケースが発生する
- インパーマネントロスが大きくなる
スワップを利用するユーザーは手数料がわずかに変わる程度なので、今これから行うスワップがV2とV3どちらの流動性を利用することになるのか気にする必要はありません。
流動性提供面では手数料報酬が集中するため、もらえる手数料報酬が増えるメリットがありますが、現在価格が価格範囲を外れると流動性が機能しなくなり、手数料が貰えません。


また、インパーマネントロスも集中して発生し、従来のパンケーキスワップV2と比べると数倍から数十倍になるので、価格変動によるリスクが大きくなっています。





BTCとUSDTを流動性として提供するときの、下限と上限価格に対応するインパーマネントロスの発生率は次の表になります。
| 下限価格 (BTC/USDT) | 現在価格 (BTC/USDT) | 上限価格 (BTC/USDT) | インパロス (通常) | インパロス (集中流動性) | 損失倍率 (通常vs集中) |
|---|---|---|---|---|---|
| 95,238 | 100,000 | 105,000 | 0.03% | 1.23% | 41.5倍 |
| 90,909 | 100,000 | 110,000 | 0.11% | 2.44% | 21.5倍 |
| 83,333 | 100,000 | 120,000 | 0.41% | 4.75% | 11.5倍 |
| 66,667 | 100,000 | 150,000 | 2.02% | 11.01% | 5.4倍 |
| 50,000 | 100,000 | 200,000 | 5.72% | 19.53% | 3.4倍 |
| 33,333 | 100,000 | 300,000 | 13.40% | 31.70% | 2.4倍 |
| 25,000 | 100,000 | 400,000 | 20.00% | 40.00% | 2.0倍 |
集中流動性インパーマネントロス 早見表
- スワップ目線では大きな変化なし
- 集中流動性の提供は利率が大きく上昇
- しかしインパロスのリスクも大きい
- 流動性提供はV3で難易度が上がった


パンケーキスワップV3とは?V2との違い


パンケーキスワップV3は「資本効率性」を高めるためにユニスワップV3をベースに開発されました。
従来のパンケーキスワップV2では流動性は0から∞の価格範囲で提供されていましたが、結局実際のスワップに利用される流動性はその内のわずかでした。


不要な流動性の提供を防げれば、流動性提供者の利率が高まるだけでなく、例えば仮想通貨CAKEであればパンケーキスワップ上での投票に回せるようになり、本来の役割をこなせるようになります。
言い換えれば、無駄な流動性は不要となったため、流動性を需要のある価格帯に適切に配置・管理する人に報酬が集中するため、ライトユーザーが「流動性マイニング」を行う機会は減ったともいえます。



パンケーキスワップV3とV2の重要な違いは次の3点です。
※主に流動性提供側にとっての違いとなり、スワップ利用者が実感する違いはほとんどありません。
ユニスワップと大枠の仕組みはまったく同じで、手数料設定などが僅かに違う程度なので、ユニスワップV3の仕様を理解している方は特に読む必要はありません。
①流動性提供時に価格範囲を決める
パンケーキスワップV3では、流動性を提供するときに価格範囲を設定する必要があります。
実際の流動性提供画面では次のような画面が表示されます。


現在価格が価格範囲内にあるときにのみあなたの流動性は機能して手数料報酬をもらえるため、現在価格付近に流動性が集中しやすくなります。
スワップ目線では現在価格付近に集中しているほど瞬発的な価格変化「プライスインパクト」が発生しづらくなり、スワップ価格が安定しやすくなります。
流動性提供者にとっては手数料報酬が集中することで利率も高くなり、価格範囲を狭くすると年間利率で100%以上になることも珍しくないです。
※従来同様0から∞でも提供できるが、報酬がほとんど貰えなくなる。



しかし「インパーマネントロス」のリスクも高まるため、価格範囲を狭くした流動性提供は上級者向けといえます。
②流動性毎にスワップ手数料が異なる
パンケーキスワップV2ではスワップ手数料が全てのスワップで一律で0.25%でしたが、パンケーキスワップV3の集中流動性では、流動性毎に発生するスワップ手数料が異なります。
各流動性ペア毎に次の4つの異なる手数料のプールが存在し、流動性を提供するときにどの手数料にするかを選択できます。


選択式ではありますが、需要が高く利用されやすい手数料設定のものに流動性は集中し、上画像はBNB/CAKEの例で0.25%の手数料に流動性の79%が集まっています。
スワップ手数料は高すぎるとユーザーはスワップを行いたくなくなり、逆にスワップ手数料が安すぎるとインパーマネントロスを上回る報酬を得られないリスクから流動性が集まらなくなります。
スワップ利用者と流動性提供の間には、各銘柄の価格変動リスク毎に丁度良い落としどころのスワップ手数料率があり、その手数料設定の流動性プールに流動性が集まる訳です。
従って、基本的には最初に自動提案された手数料で設定すれば問題ありません。



各流動性ペア毎に最も流動性が集まっている手数料設定をまとめると、次のようになります。
| 手数料率 | ペア例 |
|---|---|
| 0.01% | USDT/WBNB |
| 0.05% | ASTER&WBNB |
| 0.25% | BNB&CAKE |
| 1.00% | ZEC&USDT |
手数料率参照:2025/11/21時点
例えばステーブルコイン同士のペアはインパーマネントロスのリスクがなく、流動性提供側はスワップ手数料報酬が少なくても流動性を提供するインセンティブがあります。
スワップを利用する側も安いスワップ手数料を望んでいるので、最も安い0.01%に必然的に流動性が集まります。
③1:1で流動性を提供する必要がない
パンケーキスワップV3は「資本効率性」を目的に開発されており、1:1で流動性を提供する必要はなく、設定した価格範囲毎にパンケーキスワップが必要とする比率の流動性しか提供できません。
価格範囲の設定の仕方によっては、ペアの片方の流動性しか提供できない場合もあります。
パンケーキスワップV2では各流動性毎に全員で1つの流動性を構築しており、定積AMMと呼ばれる「xy=k」の式に従い、スワップレートや流動性の変化が決まっていました。


※xとyが流動性の枚数でkは流動性提供や削除の際にのみ再計算される定数。
集中流動性では、各流動性提供者が独自の無数のパターンの価格範囲で流動性を提供するため、1つの流動性の曲線(xy=k)では管理できません。



分かりやすくするために、3人のみでパンケーキスワップV3にBTC&USDTの流動性を提供している場合をイメージしてみましょう。
現在のBTCの価格は$60,000で、Aさん、Bさん、Cさんの3人は以下の価格範囲で流動性を提供しました。
- A:「59,000~61,000USDT」で配置(BTC&USDTの複合ポジ)
- B:「61,000USDT~∞」で配置(BTCの単一ポジ)
- C:「0~59,000USDT」で配置(USDTの単一ポジ)
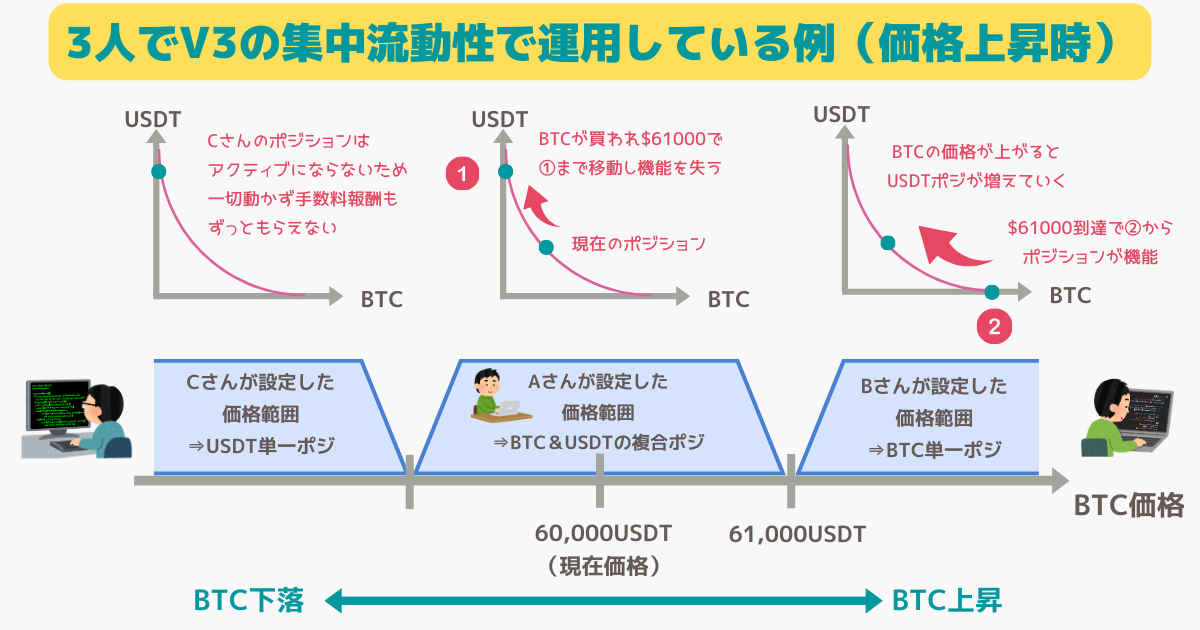

例えば、Bさんは提供する流動性の価格帯の下限を現在価格よりも大きく設定していますが、この場合は供給する流動性は全てBTCにしなければなりません。
パンケーキスワップV3の「資本効率性」の観点からすると、USDTは一切必要ないからです。
Bさんの流動性はAさんの流動性でBTCが全て買い尽くされた時にアクティブになりますが、この状態というのは流動性からBTCがなくなっており、さらにBTCを利用者に買わせてあげるにはBTCだけが必要だからです。
この時Aさんの流動性が機能しなくなりUSDTが機能していないですが、BTCが売られて価格が少しでも下がると今度はAさんの流動性が再度アクティブになり、USDTが流動性として機能するようになります。
このように、下限の価格が現在価格に近付けば近づくほど流動性として提供しなければならないUSDTの枚数は減り、逆に上限の価格が現在価格に近付けば近づくほど、必要になるBTCの枚数が減ります。



中級者~上級者向けですが、流動性提供時の枚数比率の具体的な計算式は、本記事の後半で詳しく解説しています。
【補足】パンケーキスワップV3の流動性提供の計算式


集中流動性では、次のxy=kをベースにした式(kをL二乗で表現しただけ)を変形していくことで、各流動性提供者個別の集中流動性の式を導くことができます。
\(xy=L^2\)



価格をPとすると、Pは次のように表せます。
\(P=\frac{y}{x}\)
xとyはそれぞれLとPを使って次のように表せます。
①:\(xy=L^2\)
②:\(y=Px\)
上記の2式より、
\(x=\frac{L}{\sqrt{P}}\)
\(y=L\sqrt{P}\)
この式は、ある価格区間に含まれる全ての個別の流動性の傾きL(後述)の合計と、流動性の合計x・yと、それらによって定義される価格Pの関係を表した式です。
しかし、あなたが行う集中流動性は自身で決めた価格範囲に従い、あなた特有の流動性ポジションの変化をするため、この式であなたの流動性は一切定義されません。
集中流動性の提供では価格範囲を設定し、上限または下限に達すると片方のトークンだけが残るため、この仕様を式に反映させて、あなただけの集中流動性の関係式を導く必要があります。
今回は例として、集中流動性で提供する流動性「BTC&USDT」の枚数は「BTCがx」、「USDTがy」で考えます。BTCのUSDT建価格がPです。
提供する流動性の下限価格をPb、上限価格をPaとします。
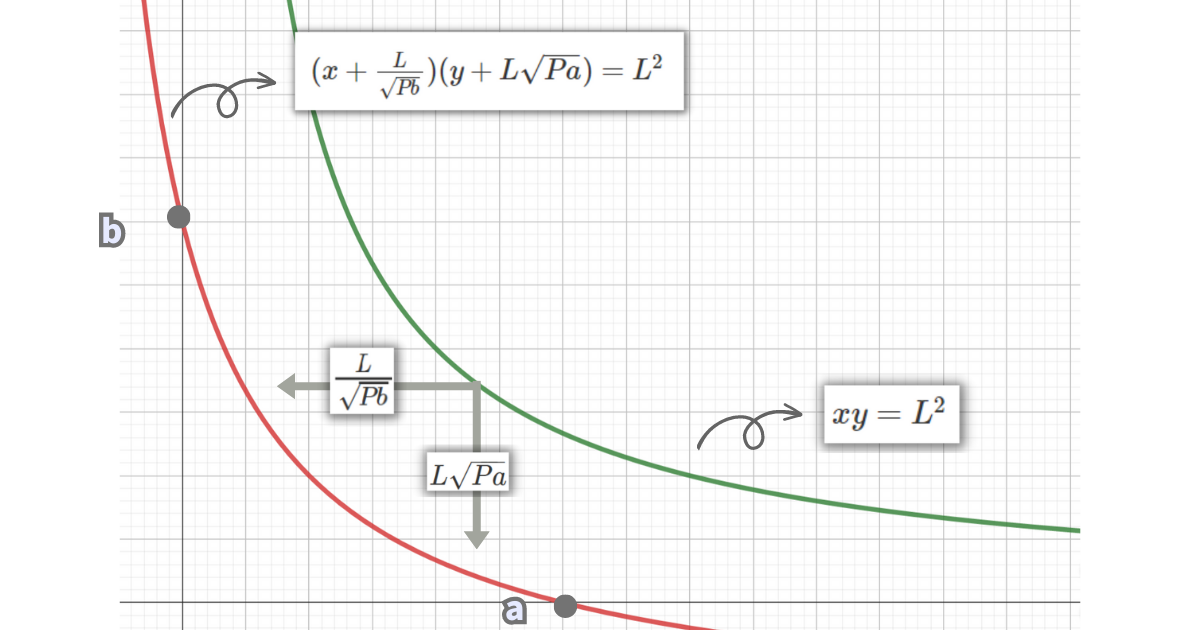
集中流動性は価格範囲を設定し、上限または下限価格で片方のトークンだけが残る仕様でしたが、これは次のようなグラフを指します。
- \(xy=L^2\)のグラフを-x方向に\(\frac{L}{\sqrt{Pb}}\)だけ平行移動する
- \(xy=L^2\)のグラフを-y方向に\(L\sqrt{Pa}\)だけ平行移動する
平行移動させたグラフとその式が次の通りです。
\((x+\frac{L}{\sqrt{Pb}})(y+L\sqrt{Pa})=L^2\)
※Lの値は最初のxy=L2のLの値とは異なり最定義されます。

ここまでの式を使い、次の条件で10,000USDTを流動性提供した時のBTCの提供枚数を求めてみます。
- 提供する流動性ペア:BTC&USDT
- 現在のBTCの価格:10,000USDT/BTC
- 流動性の上限価格:14,400USDT/BTC
- 流動性の下限価格:8,100USDT/BTC
- 提供するUSDTの枚数:10,000USDT
- 提供するBTCの枚数:?(ここを求める)
移動した式のyに10,000を入れれば良さそうですが、まだLが分かっておらず対応するxを算出できません。
※平行移動前の式はあくまでも平行移動後の式を求めるためのもので、別の式なので関係ない。Lの値も平行移動前と平行移動後では基本的に異なる。(流動性が複数存在する場合)
そこで、集中流動性で成り立つ次の2つの関係式で考えます。
\(\Delta y=L・\Delta\sqrt{P}\)
\(\Delta x=L・\Delta\frac{1}{\sqrt{P}}\)
これらは平行移動前の式から導き出せる式を変化量で定義し直しただけの式で、x・y・Pの変化の関係を表します。この式の証明は下のボックスを開くと表示されます。
上記2式の証明過程【開けます】
\(\Delta Y=L・\Delta\sqrt{P}\)
\(\sqrt{xy}=\frac{y_{1}-y_{0}}{\sqrt{P_{1}}-\sqrt{P_{0}}}\)
\(\sqrt{xy}(\sqrt{P_{1}}-\sqrt{P_{0}})=y_{1}-y_{0}\)
\(\sqrt{xy}(\sqrt{\frac{y_{1}}{x_{1}}}-\sqrt{\frac{y_{0}}{x_{0}}})=y_{1}-y_{0}\)
Virtual Curve上では、\(\sqrt{x_{1}y_{1}}=\sqrt{x_{0}y_{0}}=\sqrt{xy}=L\)のため、
\(\sqrt{\frac{x_{1}y_{1}y_{1}}{x_{1}}}-\sqrt{\frac{x_{0}y_{0}y_{0}}{x_{0}}}=y_{1}-y_{0}\)
\(\sqrt{y_{1}^2}-\sqrt{y_{0}^2}=y_{1}-y_{0}\)
\(y_{1}-y_{0}=y_{1}-y_{0}\)
Δxについても同様です。
この流動性と価格変化量の関係式は、平行移動前の式から導かれたものですが、この式は平行移動後の実際の集中流動性の式においても同じように適用でき、集中流動性における流動性の枚数変化と価格変化の関係性も表します。
ちなみに、パンケーキスワップのベースとなった「ユニスワップ公式文献」では平行移動前の式は実際の流動性の枚数関係を表さない「Virtual Curve」と呼ばれ、平行移動後の式は「Real Curve」と呼ばれます。
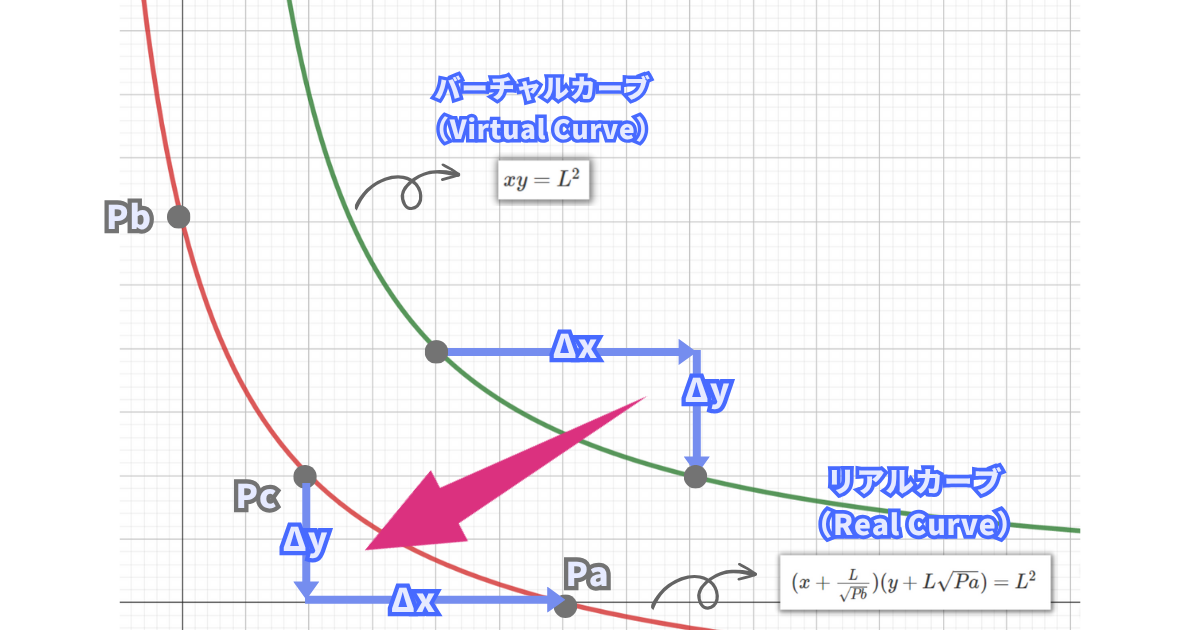

つまり、平行移動後の集中流動性の式は実際の流動性の枚数関係を表しますが、下限価格から上限価格までの流動性の枚数変化の仕方はxy=k(通常の流動性モデル、集中流動性におけるVirtual Curve)と同じになります。
集中流動性では価格範囲ごとに「独立したミニ定積AMM(xy=k)」が存在しているということです。
つまり、集中流動性のグラフにおける変化量の関係式は次のようになります。
\(\Delta x=L(\frac{1}{\sqrt{Pc}}-\frac{1}{\sqrt{Pb}})\)
\(\Delta y=L(\sqrt{Pc}-\sqrt{Pa})\)
例題の値を当てはめると次のようになります。
\(\Delta x=L(\frac{1}{\sqrt{10000}}-\frac{1}{\sqrt{14400}})\)
\(10000=L(\sqrt{10000}-\sqrt{8100})\)
最初にLが1000であることが分かり、BTCの提供枚数(Δx)=1.6666…であ
【補足】スワップが発生した場合のポジション変化の計算式


パンケーキスワップV3の集中流動性において、次の2つの流動性のみが同じ価格範囲で提供されていた場合に、スワップが行われた場合のポジションの変動について解説します。
- 提供ペア:BTC&USDT
- 現在のBTC価格:10,000USDT/BTC
- 流動性の上限価格:14,400USDT/BTC
- 流動性の下限価格:8,100USDT/BTC
- 提供するUSDTの枚数:10,000枚
- 提供するBTCの枚数:1.66667枚
- Lの値:1,000
提供するUSDTの枚数が10,000のときより、 \( \Delta y = L(\sqrt{P_{\text{現在価格}}} – \sqrt{P_{\text{下限価格}}}) \) よりL=1000と分かり、 \(\small \boldsymbol{ \Delta x = L\left( \frac{1}{\sqrt{P_{\text{現在価格}}}} – \frac{1}{\sqrt{P_{\text{上限価格}}}} \right) }\) よりxは1.66667と分かります。
- 提供ペア:BTC&USDT
- 現在のBTC価格:10,000USDT/BTC
- 流動性の上限価格:14,400USDT/BTC
- 流動性の下限価格:8,100USDT/BTC
- 提供するUSDTの枚数:1,000枚
- 提供するBTCの枚数:0.66667枚
- Lの値:100
このとき、500USDTでBTCを買うスワップが発生したときの各流動性の枚数変化を計算してみましょう。
※この価格変化は同一Tick内の微小な価格変化と仮定します。
集中流動性のTick内では次の関係式(Virtual Curve)が成り立ち、xの式は1/√Pを横軸・yの式は√Pを横軸とした場合に、Lを傾きとした1次関数の式になります。
\(xy=L^2\)
\(y=Px\)
上記の2式より、
\(x=\frac{L}{\sqrt{P}}\)
\(y=L\sqrt{P}\)
従って、
\(\Delta x=L・\Delta\frac{1}{\sqrt{P}}\)
\(\Delta y=L・\Delta\sqrt{P}\)




※xがBTCの流動性枚数、yがUSDTの流動性枚数です。例えばyの式に着目すると、提供された流動性が大きいほど傾きLの値が大きくなり、USDTでBTCにスワップした際のBTCの価格が変化が鈍くなります。
同じTick内に該当する今回の2つの流動性において√Pは同じ値を共有しているため、スワップで流動性ポジションの変化が発生した場合、2つの流動性の変化の比率(配分)は傾きLの比率と同じになります。



例えば流動性AのLが1で流動性BのLが5の場合、流動性Bは√Pの価格変化に対して5倍の流動性の変化が発生します。
今回のTick区間におけるVirtual Curve式から全体の流動性ポジションの変化・価格の変化を計算すると、次のようになります。
そしてこの全体の流動性ポジションの変化を、2つの流動性(Real Curve)に配分すると、次のようになります。
これでそれぞれの集中流動性の枚数変化を計算できました。
【補足】無数の流動性を管理するTickの概念


パンケーキスワップV3の集中流動性では、様々なパターンの価格範囲が設定された無数の流動性を管理して、AMMのスワップや価格管理を実現する必要があるため、Tick(ティック)という概念を使用します。
Tickは「ある2つの価格間の範囲」を表す概念で、Tickの区切れ目は次の式で計算されます。
※tはtick indexと呼ばれる正の整数
1.0001倍毎にTickの区切れ目があり、その間隔それぞれが1つのTickとなります。



この1つのTickそれぞれにVirtual Curveが設定されます。


しかし、流動性を構成するペアによってはあまりにも価格変動が大きく、1,0001倍毎にTickの区切りを設定する意味がない場合もあるため、実際は各ペア毎に「Tick Spacing」を定義し、数十から数百のTickをひとまとまりにします。
パンケーキスワップV3ではこのTick Spacing毎にスワップ手数料が設定される仕組みで、価格変化がほぼないステーブルコインペアなら最小のTick Spacingが設定され、ミームコインを含めば大きく設定されます。
| Tick spacing | 手数料率 | ペア例 |
|---|---|---|
| 1 | 0.01% | USDT/USDC |
| 10 | 0.05% | ASTER&WBNB |
| 50 | 0.25% | BNB&CAKE |
| 200 | 1.00% | ZEC&USDT |
Tick Spacing参照:developer docs “Fee Tier and Tick Spacing“
Tick Spacingが細かいほど、特定の価格範囲に絞った流動性の集中がより実現しやすくなります。
従って、米ドルステーブルコイン同士のスワップの場合、ユーザーは1ドル同士のスワップを望むため、Tick Spacingを狭くして1ドル周辺に流動性を集中させます。
流動性提供側の観点で考えると、インパーマネントロス発生のリスクがなく、手数料報酬を多く必要とせずに流動性を提供するインセンティブがあるため、スワップ手数料率は低く設定されます。
集中流動性では、このTick1つ1つにVirtual Curve(xy=L^2)があり、LはそのTickに該当するReal Curveの流動性の合計を表しています。


先ほど解説したように、微量のスワップが発生して1つTick内に留まる小さな価格変化が起きた場合、次のように各個人の流動性のポジション変化を計算できます。
- スワップが発生する
- Virtual Curveでx・y・Pが変化
- 各LPにx・yの変化を配分
まずはVirtual Curve式を用いてスワップによるΔx・Δy・ΔPを算出していきます。
Lは現在のTick内においてアクティブな流動性の合計となっており、現在価格は分かっているため、スワップによるΔxが入力されると、Δyとスワップ後の価格Pが計算できます。
これによりスワップによるこのTick区間の全体のx・y・Pの変化が計算できました。ここから、各Real Curve(各個人の流動性)への影響も計算できます。
Virtual CurveとReal Curveは平行移動しただけで同じ傾きのため、Virtual Curveにおける枚数変化の比率とReal Curveにおける枚数変化の比率は同じになります。
従って、TickのVirtual curveにおけるΔxとΔyを各個人Real CurveのLiで比例配分すると、各個人の流動性ポジションの変化ΔxiとΔyiが計算されます。
このように、集中流動性ではTickで価格を区分けし、各Tick毎のVirtual Curveと、そのVirtual Curveから枝分かれしたReal Curveで各個人の流動性ポジションを計算・管理している訳です。
【補足】集中流動性のインパーマネントロスの計算式


「パンケーキスワップV3のインパーマネントロスの計算式」の解説は長くなりすぎるので、下の記事をご覧ください。


下の集中流動性のインパーマネントロス(IL)の計算ツールを使うと、将来価格時点のインパーマネントロスが何パーセント発生するかを計算できます。
集中流動性 IL計算ツール
①~⑤まで入力して「計算開始」を押すと、対応する流動性枚数とインパーマネントロスが計算されます。価格は A/B(1 B あたり A) で入力してください。例:USDT/BTC = 10000



流動性の枚数は片方の入力だけで大丈夫です。もう片方の枚数は上限価格と下限価格から自動で算出されます。
【補足】PancakeSwap Infinityとの違い


PancakeSwap Infinityは、2025年4月にローンチされたパンケーキスワップV3の次のバージョンで、V3・V2の流動性と平行して運用されています。(また数は少ない)
>>パンケーキスワップ公式アナウンス “PancakeSwap Infinity is Now Live!“
元々はパンケーキスワップV4の名称で予定されていましたが、DeFiにおける無限の可能性の追求の意を込めて「Infinity」という名称に変更されました。
ユニスワップのV4に相当し、PancakeSwap Inifinityの方がより柔軟に流動性を設計できる仕組みになっています。



PancakeSwap InfinityとV3の違いは次の通りです。
| 項目 | PancakeSwap V3 | PancakeSwap Infinity |
|---|---|---|
| 対応プールタイプ | CLAMM(集中流動性) のみ | CLAMM + LBAMM(Liquidity Book) |
| トークン残高追跡 | PoolManager担当 | Vault担当(PoolManager分離) |
| プール構造 | 各プールが個別コントラクト | 単一コントラクトで全プール管理 |
| 手数料設定 | 各プール固定 | 固定 or 自動調整 |
| 拡張機能(Hook) | なし | 外部コントラクトで追加機能設定可 |
| スワップ効率 | プールごとにトークン転送(中間転送あり) | 中間プール転送不要 |
最大の特徴は、PancakeSwap Infinityでは集中流動性AMM(Concentrated Liquidity Automated Market Maker)だけでなく、LBAMM(Liquidity Book AMM)と呼ばれるAMMを利用できる点です。
LBAMMはユニスワップにもない独自のAMMで、次の特徴があります。
- 流動性は「Bin」と呼ばれる箱に入れる
- Binには番号が付いており各々特定の価格範囲
- 各Binが実際にトークン残高を保有する
Tickも下限価格と上限価格があるので大きな違いはないですが、流動性がERC-20のような代替トークンで表現され、ポジション調整が用意になっています。
その他、開発者が自分のアプリケーションに適した「フック」と呼ばれるスマートコントラクトを流動性プールにセットでき、追加の機能を付けることができます。(手数料の調整や流動性カーブのカスタマイズ等)
【補足】パンケーキスワップV3とユニスワップV3の違い


パンケーキスワップV3とユニスワップV3の機能面の違いは、ユーザーが実感できる範囲ではスワップ手数料(LP報酬手数料)が異なる点のみです。
>>参照:developer docs “What are the key differences between Uniswap v3 and PancakeSwap v3?“
パンケーキスワップV3の手数料ティアとTick Spacingの対応は次の通りです。
| Tick spacing | 手数料率 | ペア例 |
|---|---|---|
| 1 | 0.01% | USDT/USDC |
| 10 | 0.05% | ASTER&WBNB |
| 50 | 0.25% | BNB&CAKE |
| 200 | 1.00% | ZEC&USDT |
Tick Spacing参照:developer docs “Fee Tier and Tick Spacing“
ユニスワップV3の手数料ティアとTick Spacingの対応は次の通りです。
| Tick spacing | 手数料率 | ペア例 |
|---|---|---|
| 1 | 0.01% | USDC&USDT |
| 6 | 0.03% | ETH&LINK |
| 10 | 0.05% | ETH&USDC |
| 200 | 1.00% | ETH&GMX |
参照:Uniswap “What is a tick when providing liquidity?“
このように、手数料ティアとTick Spacingが違います。
また、パンケーキスワップは「仮想通貨CAKE」が一部の流動性提供の報酬に追加される特徴があります。
その代わり、スワップ手数料報酬の一部をバーンして発行量を抑えたり、トレジャリーに保管したりするエコシステムになっており、もらえる手数料報酬が次のように大体2/3になる特徴があります。
| 手数料率 | 流動性提供者 | バーン | 金庫 |
|---|---|---|---|
| 0.01% | 67% | 15% | 18% |
| 0.05% | 66% | 15% | 19% |
| 0.25% | 68% | 23% | 9% |
| 1.00% | 68% | 23% | 9% |
参照:pancakeswap.docs “Trading fees“
※パンケーキスワップとユニスワップでどちらが一概に儲かるとは言えません。
まとめ:V3の集中流動性提供は一時損失に注意


パンケーキスワップV3とV2の重要な違いは次の3点です。
スワップ目線ではスワップ手数料がわずかに変わる程度なので、変化はほとんど分からないはずです。
※大きな金額のスワップでは「プライスインパクト」の軽減を実感できる。
流動性を提供するときは利率が大きく高まりますが、価格範囲を外れると報酬が入らなくなり、インパーマネントロスリスクも高まるため注意が必要です。
- スワップ目線では大きな変化なし
- 集中流動性の提供は利率が大きく上昇
- しかしインパロスのリスクも大きい
- 流動性提供はV3で難易度が上がった



ご覧いただきありがとうございました。
本記事に関するご質問・ご感想はコメント欄か下記のお問い合わせページ・XのDMよりお送り下さい。丁寧に回答させていただきます。
メールアドレスはこちら:contact@pandacrypto.xsrv.jp

ご覧いただきありがとうございました。
本記事に関するご質問・ご感想はコメント欄か下記のお問い合わせページ・XのDMよりお送り下さい。丁寧に回答させていただきます。
メールアドレスはこちら:contact@pandacrypto.xsrv.jp
※2020年5月1日より「仮想通貨」は「暗号資産」へ呼称変更されていますが、一部記事では「仮想通貨」の表記を継続する場合があります。当サイトの「仮想通貨」は「暗号資産」を指します。
仮想通貨に関する注意喚起

仮想通貨の価格は日々変動しており、保有する仮想通貨の価格が急激に下落する場合があります。購入時の価格を下回ったり、無価値になってしまうことで大きな損失が発生する恐れがあります。
仮想通貨の信用取引は、価格変動により保証金を上回る損失が発生する場合があります。
その他仮想通貨に関する注意喚起について詳しく知りたい方は、以下をご覧ください。
| 金融庁 | 暗号資産の利用者のみなさまへ |
| 警察庁 | 暗号資産(仮想通貨)に関するトラブルにご注意ください! |
| 消費者庁 | 投資などのお金に関するトラブルや悪質商法について |
| 国税庁 | 仮想通貨の税務上の取扱い-現状と課題- |
| 政府広報オンライン | 暗号資産の「必ずもうかる」に要注意! |
| 日本暗号資産取引業協会 | 暗号資産に関するトラブルにご注意ください! |
| 国民生活センター | 暗号資産に関する消費者トラブル |






コメント